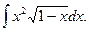|
|
Метод замены переменной (метод подстановки)
Если неопределенный интеграл непосредственно не берется, то во многих случаях замена переменной интегрирования приводит к более простому интегралу
Пусть функция 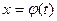 определена и дифференцируема на сегменте
определена и дифференцируема на сегменте 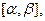 а множество ее значений принадлежит сегменту [a,b] . Пусть функция y =f(x) определена на [a,b] и имеет на этом сегменте первообразную F(x). Тогда имеет место формула
а множество ее значений принадлежит сегменту [a,b] . Пусть функция y =f(x) определена на [a,b] и имеет на этом сегменте первообразную F(x). Тогда имеет место формула
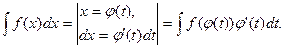
Полученная формула называется формулой замены переменной в неопределенном интеграле.
После интегрирования нового интеграла полученная функция является функцией переменной t. Для возвращения к переменной х необходимо заменить t значением  которое находится из соотношения
которое находится из соотношения 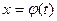 .
.
Пример.Найти интеграл .
.
Решение.  =
= 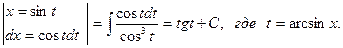
Частным случаем метода замены переменной интегрирования является метод подведения под знак дифференциала. Пусть требуется найти интеграл  . Предположим, что существует дифференцируемые функция
. Предположим, что существует дифференцируемые функция  и функция
и функция 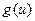 такие, что подынтегральное выражение
такие, что подынтегральное выражение 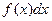 может быть представлено в виде
может быть представлено в виде
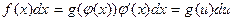
(указанное преобразование называется подведением  под знак дифференциала). Тогда
под знак дифференциала). Тогда
 ,
,
т.е. нахождение интеграла  сводится к нахождению интеграла
сводится к нахождению интеграла 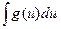 (который может оказаться проще данного) и последующей подстановке
(который может оказаться проще данного) и последующей подстановке  .
.
Полезно запомнить частный случай

Интеграл дроби, числитель которой есть дифференциал знаменателя, равен натуральному логарифму модуля знаменателя.
Особенно широко применяется метод введения под знак дифференциала в том случае, когда аргументом подынтегральной функции является линейна функция от переменной интегрирования.
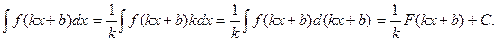
Пример.Найти интеграл 
Решение. 
Пример.Найти интеграл 
Решение. 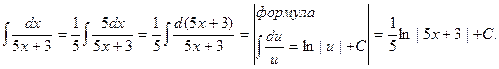
Упражнения
1. 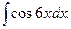 2.
2. 
3. 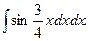 4.
4. 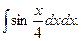
5.  . 6.
. 6. 
7. 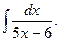 8.
8. 
9. 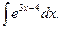 10.
10. 
11.  12.
12. 
13. 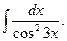 14.
14.  .
.
15.  . 16.
. 16. 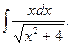
17.  18.
18. 
19. 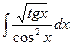 20.
20. 
21. 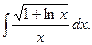 22.
22. 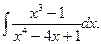
23. 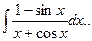 24.
24. 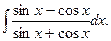
25. 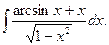 26.
26. 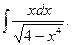
27. 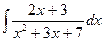 28.
28. 
29.  30.
30. 
31.  32.
32. 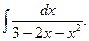
337. 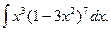 . 34.
. 34. 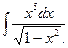
35.  . 36.
. 36. 
37.  38.
38. 
39. 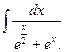 40.
40.