 |
|
Интегрирование выражений, содержащих тригонометрические функции
1) Интеграл  . Функция R(sinx,cosx) есть рациональная функция относительно sinx, cosx. Тогда интеграл
. Функция R(sinx,cosx) есть рациональная функция относительно sinx, cosx. Тогда интеграл  рационализируется с помощью универсальной тригонометрической подстановки
рационализируется с помощью универсальной тригонометрической подстановки 
 =
= 
Универсальная тригонометрическая подстановка приводит часто к сложным рациональным функциям. Поэтому в ряде случаев более удобны другие подстановки:
а) функция R(sinx.cosx) есть нечетная функция относительно sinx.
 Применяется подстановка t=cosx.
Применяется подстановка t=cosx.
б) функция R(sinx.cosx) есть нечетная функция относительно cosx.
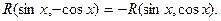 Применяется подстановка t=sinx
Применяется подстановка t=sinx
в) функция R(sinx.cosx) есть четная функция относительно sinx и cosx.
 Применяется подстановка t=tgx.
Применяется подстановка t=tgx.
2) Интегралы вида 
а) Если хотя бы одно из чисел m или n –положительное нечетное число, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы 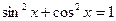 оставшуюся четную степень через дополнительную функцию, приходим к табличному интегралу.
оставшуюся четную степень через дополнительную функцию, приходим к табличному интегралу.
Пример.Найти интеграл 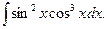

б) Если же m и n четные неотрицательные числа, то степени понижаются с помощью тригонометрических формул:
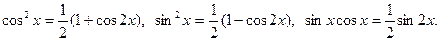
Пример.Найти интеграл 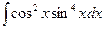

3) Интегралы вида 
преобразуются к табличным интегралам с помощью формул
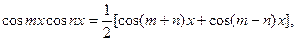


Примеры.Найти интегралы:


3) 
Упражнения
1. 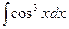 2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 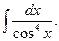
11.  12.
12. 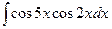

13.  14.
14. 
15. 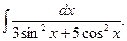 16.
16. 
Интегрирование иррациональных функций.
Основным приемом для нахождения неопределенных интегралов от иррациональных функций является рационализация подынтегральной функции с помощью замены переменной интегрирования. В зависимости от вида подынтегральной функции применяются различные подстановки.
1) 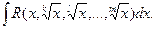 Функция R является рациональной относительно указанных величин. Подынтегральная функция рационализируется с помощью подстановки.
Функция R является рациональной относительно указанных величин. Подынтегральная функция рационализируется с помощью подстановки. 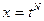 , где N – наименьшее общее кратное чисел {k, l, …, m)
, где N – наименьшее общее кратное чисел {k, l, …, m)
2) Интегрирование дробно-линейных иррациональностей.
Интеграл вида 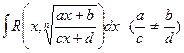 рационализируется с помощью подстановки
рационализируется с помощью подстановки 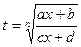 .
.
3) Нахождение интегралов вида
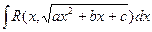 ,
,
где R – рациональная функция двух аргументов, производится с помощью тригонометрических подстановок следующим образом. Выделением полного квадрата в квадратном трехчлене с последующей заменой переменной  исходный интеграл приводится (в зависимости от знака а и дискриминанта квадратного трехчлена) к интегралу одного из следующих трех типов:
исходный интеграл приводится (в зависимости от знака а и дискриминанта квадратного трехчлена) к интегралу одного из следующих трех типов:
1) 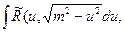 применяется подстановка
применяется подстановка  ;
;
2) 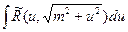 , применяется подстановка
, применяется подстановка 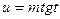 ;
;
3)  , применяется подстановка
, применяется подстановка 
Примеры.Найти интегралы.
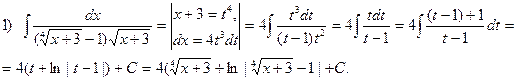
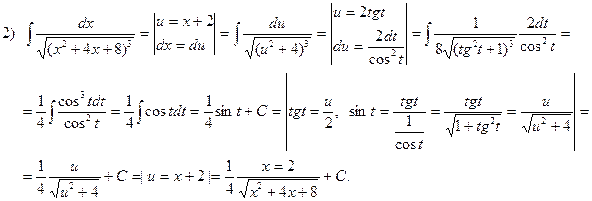
Упражнения
1.  2.
2.  .
.
3.  4.
4. 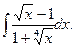
5. 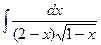 6.
6. 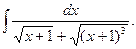
7. 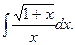 8.
8. 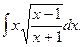
9.  10.
10. 
11. 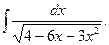 12.
12. 