Главная | Обратная связь

Интерференция прямых и обратных волн

При наличии прямой (падающей) и обратной (отраженной) волны наблюдается физическое явление интерференции. Рассмотрим результат наложения прямой и обратной волн напряжения, бегущих в противоположных направлениях

(10.22)

где

На основании принципа суперпозиции двух волн одинаковой частоты выражение (10.22) можно записать в виде

 

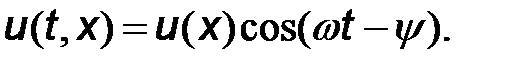(10.23)

Здесь

(10.24)

 

описывают распределение результирующей амплитуды вдоль линии (интерференционную картину) и их начальных фаз, а

(10.25)

– разность начальных фаз прямой и обратной волн.

Сомножитель третьего слагаемого в (10.24) определяет положение максимумов и минимумов интерференционной картины. Вдоль линии в местах, где выполняется условие

, n=0, 1, 2,… (10.26)

 

наблюдаются максимумы, равные , а в местах, где выполняется условие

, n=0, 1, 2,… (10.27)

 

наблюдаются минимумы, равные . Положения максимумов и минимумов вдоль линии определяются, как следует из (10.26) и (10.27), выражениями

. (10.28)

 

Следует отметить, что в максимумах мощность результирующей волны больше суммы мощностей прямой и обратной волн, а в минимумах мощность результирующей волны меньше разности их мощностей. Это указывает на то, что интерференция волн приводит к распределению мощности вдоль линии. Распределение результирующей амплитуды вдоль линии является периодической функцией. В результате этого соседние максимумы (минимумы) наблюдаются на расстояниях , а минимумы наблюдаются на расстояниях от ближайших максимумов.

В линии без потерь и с очень малыми потерями все максимумы и минимумы одинаковы по амплитуде. На практике для оценки степени согласования нагрузки с линией вводится параметр коэффициент стоячей волны по напряжению (КСВН)

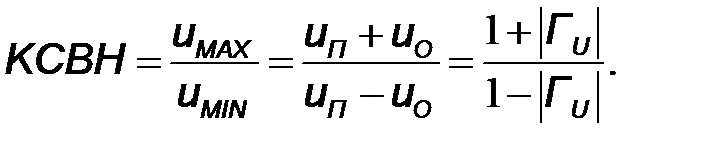(10.29)

 

Используя формулы (10.20), (10.21) и (10.29), определим характерные значения коэффициентов отражения и режимы длинной линии при разных значениях сопротивления нагрузки Z_Н.

Если сопротивление нагрузки равно волновому сопротивлению длинной линии Z_Н=Z_В, то такая нагрузка называется согласованной, при этом . В длинной линии существует только падающая волна. Такой идеальный режим переноса энергии от генератора в нагрузку называется режимом бегущей волны.

Если Z_Н=0 (короткое замыкание на конце линии), тогда 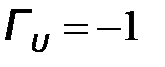, а . В этом случае на конце линии амплитуды отраженных волн напряжения и тока равны амплитудам падающих волн напряжения и тока. При этом отраженная и падающая волны напряжения находятся в противофазе, а отраженная и падающая волны тока – синфазные.

Если Z_Н= (линия разомкнута на конце, холостой ход), тогда , а . В этом случае на конце линии амплитуды отраженных волн напряжения и тока тоже равны амплитудам падающих волн напряжения и тока. Однако отраженная и падающая волны напряжения – синфазные, а отраженная и падающая волны тока находятся в противофазе.

В случаях, когда амплитуды отраженных и падающих волн равны, то есть , в линии наблюдается режим стоячих волн.

Когда сопротивление нагрузки является активным Z_Н=R_H и не равным , то и 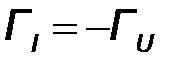. В этом случае на конце линии амплитуды отраженных волн меньше амплитуд падающих волн и в линии наблюдается режим смешанных волн. Распределения амплитуд напряжения и токов в окрестности конца линии при разных значениях сопротивления нагрузки Z_Н показаны на рис. 10.3.

 

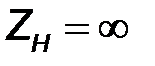
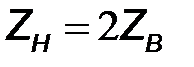
Рис. 10.3. Распределения и в окрестности конца линии