Главная | Обратная связь

Способ, основанный на представлении рассматриваемой системы совокупностью функциональных узлов

 

Представим рассматриваемую систему совокупностью функциональных узлов (рис. 10.8б), каждый из которых определяется своим коэффициентом передачи.

Первый узел проясняет, как генератор возбуждает в начале линии прямую волну. Соответствующий коэффициент передачи первого узла 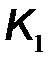назовем коэффициентом возбуждения линии . Так как цепь, моделирующая этот процесс – делитель напряжения, образованный комплексными сопротивлениями и 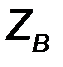, имеем

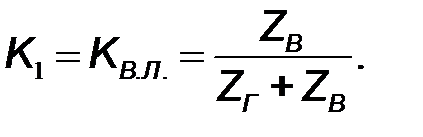
(10.35)

 

Второй узел представляет распространение прямой волны от начала линии (x=0) к ее концу (x=l), и определяется коэффициентом передачи

 

(10.36)

 

Третий узел представляет отражение прямой волны от правого конца линии, и определяется по формуле (10.20) коэффициентом отражения от нагрузки

 

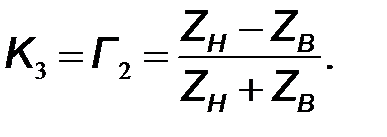
(10.37)

 

Четвертый узел представляет распространение обратной (отраженной) волны от конца линии к ее началу ( 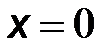) и определяется по формуле (2.26) коэффициентом передачи

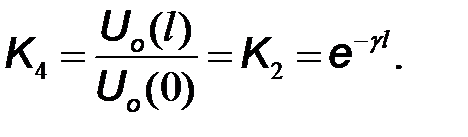(10.37)

 

Пятый узел представляет отражение обратной волны от левого конца линии ( 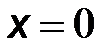), и определяется по формуле (10.20) коэффициентом отражения

 

.

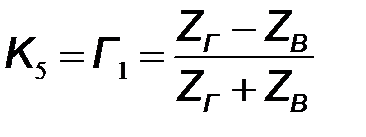(10.39)

 

а)

 

 

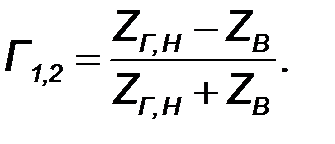
б)

 

 

в)

Рис.10.8. К выводу коэффициента передачи системы с длинной линией:

а) схема рассматриваемой системы;

б) функциональная схема системы;

в) график, поясняющий распространение и отражение волн в системе

 

Обратная волна, отражаясь от левого конца линии, становится прямой и складывается с волной, возбужденной генератором. Очевидно, что в рассматриваемой системе имеется обратная связь, образованная вторым, третьим, четвертым и пятым узлами. При этом второй узел фактически служит звеном прямой передачи, а третий, четвертый и пятый – образуют звено обратной связи. Результирующий коэффициент передачи этих узлов системы определяется известным для цепей с обратными связями выражением

 

,

(10.40)

 

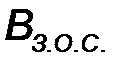где и – комплексные коэффициенты передачи звеньев прямой передачи и обратной связи. Используя эту формулу, получим

 

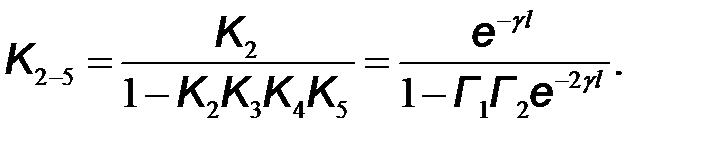(10.41)

 

Шестой узел проясняет, как прямая волна в конце линии возбуждает колебания в нагрузке. Соответствующий коэффициент передачи шестого узла 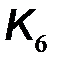назовем коэффициентом возбуждения нагрузки 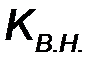. Для его определения представим длинную линию эквивалентным генератором с источником напряжения. Его задающее напряжение определяется режимом «холостого хода», то есть напряжением на конце разомкнутой линии. Ранее было получено, что оно равно . Сопротивление эквивалентного генератора равно волновому сопротивлению линии 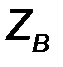. Цепь, моделирующая этот процесс – делитель напряжения, образованный комплексными сопротивлениям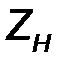и и 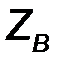. С учетом указанного удвоения амплитуды напряжения падающей волны, имеем

 

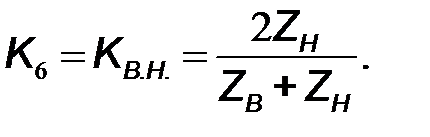
(10.42)

 

Результирующий комплексный коэффициент передачи системы в соответствии с ее функциональной схемой определяется выражением

 

.

 

С учетом выражений, полученных для коэффициентов передачи отдельных узлов, окончательно имеем:

(10.43)

 

10.4.3. Способ, основанный на использовании граничных условий

 

Второй способ, позволяющий найти эту формулу, заключается в использовании граничных условий для определения комплексных коэффициентов 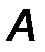и , входящих в общее решение (10.7), (10.8) уравнения Гельмгольца. Граничное условие для левого конца линии ( =0) определяется выражением

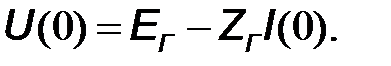
(10.44)

 

Полагая в формулах (10.7) и (10.8) 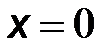получим

 

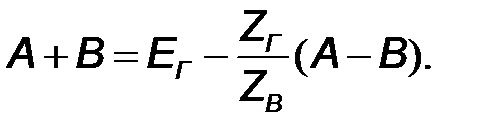
Отсюда следует

(10.46)

Граничное условие для правого конца линии определяется выражением

 

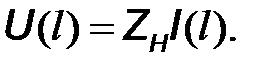(10.46)

 

Полагая в формулах (10.7) и (10.8) 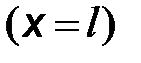, получим

 

Отсюда следует

 

(10.47)

Выражения (10.46) и (10.47) представим системой линейных алгебраических уравнений

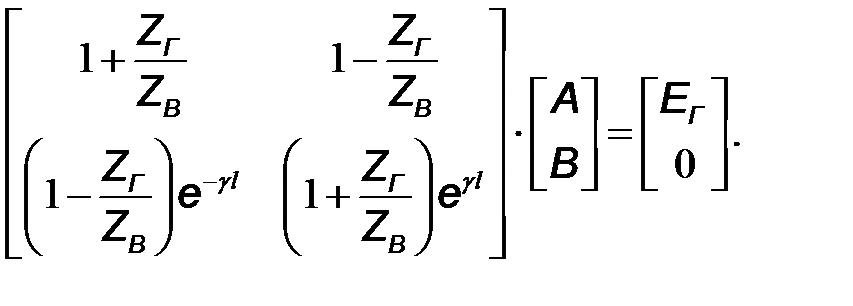(10.48)

Посредством правила Крамера и, используя введенные выше коэффициенты, находим

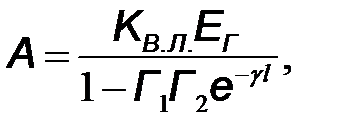
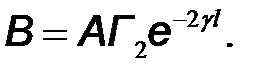(10.49)

 

Представим комплексный коэффициент передачи системы в виде

 

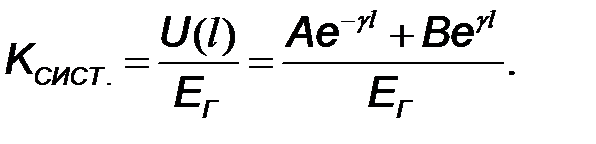(10.50)

 

Подставляя сюда найденные коэффициенты и 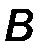, получим формулу, совпадающую с выражением (10.43), выведенным предыдущим способом.

Осуществим преобразование этой формулы. Входящий в ее состав сомножитель с учетом неравенства 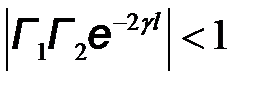представим бесконечным рядом по формуле геометрической прогрессии 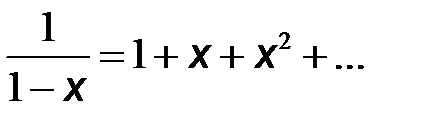, где . После подстановки ряда в (10.43) получим

 

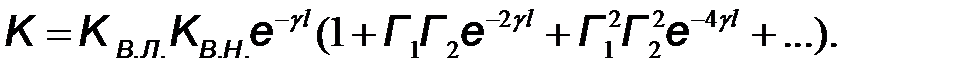(10.51)

 

Последнее выражение имеет простой физический смысл. Выходной сигнал формируется в результате наложения многократных отражений входного сигнала от концов длинной линии. Иллюстрация этого процесса представлена на рис. 10.8в.

Выражением, определяющим комплексную передаточную функцию рассматриваемой системы, является полученная формула (10.43), в которой следует использовать конкретные частотные зависимости комплексных сопротивлений 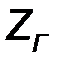, , 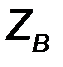. В общем случае она принимает вид

 

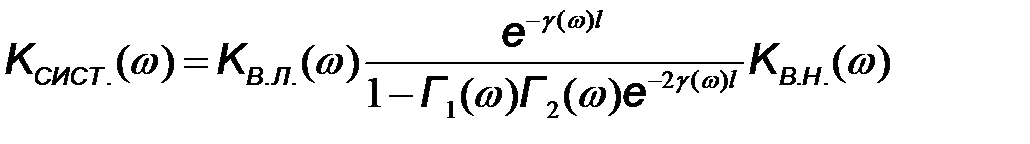. (10.52)