 |
|
Пример построения интерференционной картины
Интерференционная картина строится при заданных параметрах длинной линии и нагрузки. Таким образом, интерференционная картина – это графическое изображение зависимости  от координаты
от координаты  .
.
Рассмотрим пример построения графика зависимости  . Для этого необходимо иметь чистый лист бумаги в клеточку, карандаш, линейку и калькулятор. Пусть дано:
. Для этого необходимо иметь чистый лист бумаги в клеточку, карандаш, линейку и калькулятор. Пусть дано:
длина волны  (8 клеток); линия длиной
(8 клеток); линия длиной  (16 клеток); волновое сопротивление линии равно
(16 клеток); волновое сопротивление линии равно  ; затухание вдоль линии составляет
; затухание вдоль линии составляет 
 сопротивление нагрузки
сопротивление нагрузки 
 возбуждающий генератор согласован с линией
возбуждающий генератор согласован с линией  . Амплитуда падающей волны в начале линии
. Амплитуда падающей волны в начале линии  =10В (1 клеточка соответствует 1 В).
=10В (1 клеточка соответствует 1 В).
Чтобы получить график интерференционной картины будем выполнять расчеты и построения по следующему алгоритму.
1. Делаем заготовку графика: В начале линии при  =0 откладываем напряжение прямой волны
=0 откладываем напряжение прямой волны  =10
=10  , а при
, а при  =16 клеток откладываем ее напряжение в конце линии
=16 клеток откладываем ее напряжение в конце линии 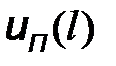 =10
=10  0,8=8 клеток.
0,8=8 клеток.
2. Рассчитываем комплексный коэффициент отражения и определяем его модуль и аргумент
 .
.
3. Рассчитываем амплитуду отраженной волны сначала в конце линии  =5,6, а затем в начале линии
=5,6, а затем в начале линии  =5,6
=5,6  0,8= =4,48
0,8= =4,48  4,5.
4,5.
4. Рассчитываем значения максимумов и минимумов для начала и конца линии. В начале линии при  имеем максимум
имеем максимум  =14,5 клетки и минимум
=14,5 клетки и минимум 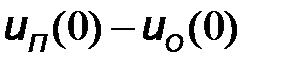 =5,5 клетки. В конце линии при
=5,5 клетки. В конце линии при  получаем
получаем  =13,6 и
=13,6 и  =2,4.
=2,4.
5. Определяем графически положение максимумов  и минимумов
и минимумов  . Для этого используя приближенное представление функции затухания
. Для этого используя приближенное представление функции затухания  линейной зависимостью, соединяем точки максимумов и минимумов в начале и в конце линии прямыми линиями.
линейной зависимостью, соединяем точки максимумов и минимумов в начале и в конце линии прямыми линиями.
6. Начинать строить график удобно с конца линии. Прежде всего, надо определить амплитуду и фазу результирующего напряжения от сложения падающей и отраженной воны на конце линии. Для этого на комплексной плоскости откладываем вектор комплексной амплитуды падающей волны  вдоль положительного направления действительной оси. Затем откладываем вектор комплексной амплитуды отраженной волны
вдоль положительного направления действительной оси. Затем откладываем вектор комплексной амплитуды отраженной волны  . Строим суммарный вектор U(l). Определяем его длину |U(l)| и начальную фазу.
. Строим суммарный вектор U(l). Определяем его длину |U(l)| и начальную фазу.
7. Определяем вид ближайшего к концу линии экстремума. Для этого рекомендуем сначала построить биссектрису угла  . В данном примере
. В данном примере  . Затем определяем, каким будет ближайший к концу линии экстремум. Для этого учитываем, что, смещая рассматриваемую точку
. Затем определяем, каким будет ближайший к концу линии экстремум. Для этого учитываем, что, смещая рассматриваемую точку  от конца линии к ее началу, вектор
от конца линии к ее началу, вектор  разворачивается на векторной диаграмме по часовой стрелке (прямая волна достигает точки
разворачивается на векторной диаграмме по часовой стрелке (прямая волна достигает точки  раньше), а вектор
раньше), а вектор 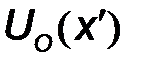 – против часовой стрелки (обратная волна достигает точки
– против часовой стрелки (обратная волна достигает точки  позже). Таким образом, ближайшим к концу экстремумом может оказаться, в первом случае – максимум, (если векторы
позже). Таким образом, ближайшим к концу экстремумом может оказаться, в первом случае – максимум, (если векторы  и
и  первоначально станут коллинеарными), во втором случае – минимум (если векторы
первоначально станут коллинеарными), во втором случае – минимум (если векторы  и
и  первоначально станут противоположно ориентированными). В рассматриваемом примере ближайшим к концу экстремумом является максимум. При этом суммарный вектор на диаграмме будет ориентирован под углом, равным биссектрисе угла φ, т. е. φ/2 = – π/8.
первоначально станут противоположно ориентированными). В рассматриваемом примере ближайшим к концу экстремумом является максимум. При этом суммарный вектор на диаграмме будет ориентирован под углом, равным биссектрисе угла φ, т. е. φ/2 = – π/8.
8. Определяем расстояние до ближайшего экстремума, учитывая, что повороту вектора на диаграмме на угол, равный 2π, соответствует отрезок линии, равный длине волны λ (λ = 2π рад.). В первом случае расстояние на графике до максимума определит угол, отсчитываемый от действительной положительной полуоси до упомянутой биссектрисы. Во втором случае расстояние на графике до минимума определит угол, отсчитываемый от действительной положительной полуоси до линии, перпендикулярной к упомянутой биссектрисе. В данном примере ближайший к концу линии максимум расположится на расстоянии π/8 рад, т. е. на расстоянии λ/16 (одна клетка от конца линии).
9. Расположение найденного экстремума определяет положения всех остальных. Учитывая, что расстояние между соседними максимумами (минимумами) равно λ/2 (8 клеток), откладываем на линиях  и
и  точки максимумов и минимумов.
точки максимумов и минимумов.
10. Соединяем точки экстремумов линией, представляющей график  .
.
Результат построения распределения  показан на рис. 10.4.
показан на рис. 10.4.

Рис. 10.4. Распределение  полученное в результате интерференции падающей и отраженной волн рассмотренного примера
полученное в результате интерференции падающей и отраженной волн рассмотренного примера