 |
|
Задача модального керування
Динамічні властивості системи автоматичного управління визначаються коріннями характеристичного рівняння 
, яким, у свою чергу, відповідають складові вільного руху системи, які називають «модами» 
.
Модальне керування – це таке керування, коли досягається потрібний характер перехідних процесів за рахунок забезпечення необхідного розташування коренів характеристичного полінома на комплексній площині. При цьому задача зводиться до визначення коефіцієнтів відповідних зворотних зв'язків за станом об'єкта. Модальне керування застосовується тоді, коли всі складові вектора стану об'єкта доступні для безпосереднього вимірювання.
Розглянемо послідовність розв’язання задачі модального керування.
Нехай повністю керований і спостережуваний об'єкт заданий моделлю в просторі станів (1.1), яка має вигляд канонічної нормальної форми. Розмірність вектора керуючих впливів дорівнює 
, тобто керування є скалярним.
Сформуємо зворотний зв'язок за станом наступним чином:
, (1.2)
де 
– вектор-рядок коефіцієнтів зворотних зв'язків.
Тоді, підставивши рівняння (1.2) в (1.1), одержимо рівняння динаміки замкненої системи:
(1.3)
Характеристичний поліном отриманої замкненої системи визначається наступним чином:
. (1.4)
Тоді задача модального керування може бути сформульована таким чином: для керованої системи (1.1) з характеристичним поліномом знайти вектор коефіцієнтів зворотних зв'язків 
такий, щоб замкнена система (1.3) мала бажану стандартну форму характеристичного полінома (1.4).
Процедура розрахунку коефіцієнтів зворотних зв'язків виконується наступним чином.
Вибирається бажане розташування коренів характеристичного рівняння замкненої системи 
. Для цього використовуються наступні співвідношення.
Тривалість перехідного процесу оцінюється за ступенем стійкості 
замкненої системи. Так називається відстань від самого правого кореня характеристичного рівняння до уявної осі. Зазвичай приймається
,
де 
– величина допустимої помилки.
Таким чином, при обмеженні лише на 
область допустимого розташування коренів 
уявляє собою напівплощину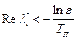 
.
Число 
називають коливальністю системи, величина якої визначається як тангенс кута розкриття сектора, усередині якого лежать усі полюси системи 
.
Перерегулювання (у відсотках) оцінюється за формулою
.
Кожному значенню перерегулювання відповідає свій сектор, який обмежує розташування полюсів.
Таким чином, при використанні двох обмежень (перше – на , друге – на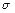 
) область допустимого розташування коренів характеристичного рівняння замкненої системи уявляє собою усічений сектор в лівій напівплощині комплексної площини.
Після вибору полюсів замкненої системи обчислюють її характеристичний поліном за допомогою формули
.
Прирівнюючи поліноми 
та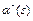 
, отримані на першому та другому кроках, отримуємо рівняння для визначення невідомих коефіцієнтів зворотних зв'язків
,
звідки отримуємо:
. (1.5)
Таким чином, при можливості вимірювання всіх компонент вектора стану об’єкта за допомогою вибору коефіцієнтів зворотних зв'язків за формулою (1.5) можна отримати будь-яке бажане розташування полюсів замкненої системи.