ПРИКЛАД ВИКОНАННЯ РОЗРАХУНКОВОГО ЗАВДАННЯ

Нехай об'єктом керування є динамічна система, що складається з двох вантажів з масами кг і кг, які з'єднані двома пружинами, жорсткості яких дорівнюють кг/с² і кг/с² (див. рис. 3.1).

Рисунок 3.1 – Схема динамічної системи «два вантажа,

які з'єднані пружинами»

Нехай і – це горизонтальне відхилення першого та другого вантажів від положення рівноваги в момент часу . Тоді рух вантажів описується наступними диференціальними рівняннями:

де – керуючий вплив.

Виходом об'єкта вважається переміщення другого вантажу . У початковий момент часу відхилення другого вантажу від положення рівноваги становить см.

Послідовність виконання розрахункового завдання

1. Для того, щоб знайти передавальну функцію системи, спочатку обчислимо перетворення Лапласа від лівих та правих частин диференціальних рівнянь

виразимо змінну з другого рівняння та підставимо в перше:

Оскільки виходом об’єкта є змінна , то передавальна функція буде мати вигляд

Після приведення до стандартного виду отримаємо:

2. Для побудови графіка перехідної характеристики об'єкта впродовж 50 секунд при нульових початкових умовах і дослідження впливу величини жорсткості першої пружини створимо наступний m-файл:

>> m1 = 1; m2 = 2;

>> c1 = 2; c2 = 1;

>> num = m1*m2/c2;

>> figure (1);

>> string1 = ['b', 'r', 'g'];

>> string2 = ['-', ':', '.-'];

>> for i = 1:1:3

>> c1 = c1+0.5*(i-1);

>> den=[1 0 c1/m1+c2*(1/m1+1/m2) 0 c1*c2/(m1*m2)];

>> f = tf ( num, den );

>> step(f, strcat(string1(i), string2(i)), 50);

>> hold on;

>> end;

>> legend ('c_1 = 1.0', 'c_1 = 1.5', 'c_1 = 2.0');

Результат зображено на рис. 3.2.

Аналіз графіка дозволяє зробити висновки, що при дії одиничного сигналу на виході системи встановлюються автоколивання, а при збільшенні

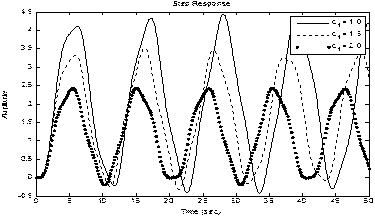
Рисунок 3.2 – Графік впливу жорсткості пружини на вид

перехідної характеристики об’єкта

жорсткості пружини зменшуються амплітуда та період коливань другого вантажу.

3. Для побудови амплітудно-частотних характеристик об'єкта створимо наступний m-файл:

>> c1 = 2;

>> den = [1 0 c1/m1+c2*(1/m1+1/m2) 0 c1*c2/(m1*m2)];

>> system = tf ( num, den );

>> figure (2);

>> bode ( system );

>> grid on;

Результат зображено на рис. 3.3. Аналіз отриманих графіків дозволяє встановити, що досліджуваний діапазон частот, у якому змінюються характеристики об’єкта складає рад/сек

Для дослідження впливу маси 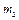на вид логарифмічної амплітудно-частотної характеристики об'єкта створимо наступний m-файл:

>> figure (3);

>> for i = 1:1:3

>> m2 = m2+0.5*(i-1);

>> num = m1*m2/c2;

Рисунок 3.3 – Графік логарифмічних АЧХ та ФЧХ об’єкта

>> den=[1 0 c1/m1+c2*(1/m1+1/m2) 0 c1*c2/(m1*m2)];

>> system = tf ( num, den );

>> w = logspace (-1, 1, 5000);

>> r = freqresp(system, w);

>> r = r(:);

>> loglog(w,abs(r),strcat(string1(i),string2(i)));

>> hold on;

>> end;

>> legend ('m_2 = 2.0', 'm_2 = 2.5', 'm_2 = 3.0');

Результат зображено на рис. 3.4.

Аналіз графіка дозволяє зробити висновок, що об’єкт є фільтром низьких частот з двома резонансними частотами. При збільшенні маси другого вантажу збільшується коефіцієнт передачі на низьких частотах та зменшується значення першої резонансної частоти.

4. Для розв’язання задачі реалізації об'єкта в просторі станів у вигляді канонічної нормальної форми треба визначити, чи має нулі передавальна функція об’єкта. В нашому випадку ступінь полінома в чисельнику дорівнює нулю, тобто ПФ нулів не має.

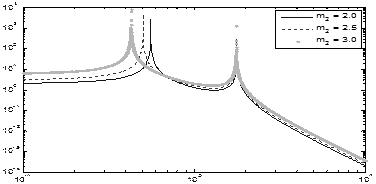
Рисунок 3.4 – Графік впливу маси вантажу 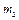на вид ЛАЧХ об’єкта

Модель системи у просторі станів має вигляд

а матриці у нормальній формі мають такі значення:

5. Щоб нарисувати структурну схему отриманої реалізації, треба записати рівняння моделі для кожної змінної:

Рисунок 3.5 – Структурна схема об’єкта керування

6. Для побудови моделі у просторі станів створимо наступний m-файл:

>> A = [ 0 1 0 0; …

0 0 1 0; …

0 0 0 1; …

-c1*c2/(m1*m2) 0 -c1/m1-c2*(1/m1+1/m2) 0];

>> B = [ 0; 0; 0; m1*m2/c2];

>> C = [1 0 0 0];

>> system_ss = ss ( A, B, C, 0 );

Для побудови графіка руху об’єкта при заданих ненульових початкових умовах см створимо наступний m-файл:

>> x0 = [ 0; 0; 0; 0.5];

>> t = 0:0.01:50;

>> u = zeros(1, length(t));

>> figure (4);

>> lsim (system_ss, u, t, x0 );

Результат зображено на рис. 3.6.

7. Для перевірки виконання умови керованості застосуємо алгебраїчний критерій: об’єкт є керованим, якщо ранг матриці керованості Калмана дорівнює порядку системи.

Створимо наступний m-файл:

>> Kalman = [B A*B A*A*B A*A*A*B];

>> r = rank ( Kalman )

Рисунок 3.6 – Графік руху об’єкта при ненульових початкових умовах

В результаті отримаємо наступну відповідь:

r =

Таким чином, об’єкт є керованим.

8. Треба розв’язати задачу модального керування так, щоб виконувалися наступні вимоги до якості перехідного процесу в замкненій системі:

а) точність см;

б) тривалість перехідного процесу не більше с;

в) коливальність дорівнює .

Виходячи з заданих вимог, виберемо розташування полюсів замкненої системи:

Остаточно обираємо такі значення:

Обчислимо коефіцієнти бажаного характеристичного полінома замкненої системи:

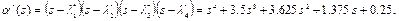
Обчислимо коефіцієнти характеристичного полінома об’єкта:

За формулою (4.4) обчислимо коефіцієнти зворотного зв’язку:

Таким чином, матриця коефіцієнтів зворотного зв’язку має вигляд:

9. Для побудови графіка перехідного процеса в замкненій системі створимо наступний m-файл:

>> K = [-0.375 0.6875 0.0625 1.75];

>> A1 = A - B*K;

>> system_feedback = ss ( A1, B, C, 0);

>> figure (5);

>> step ( system_feedback );

Рисунок 3.7 – Графік перехідного процеса в замкненій системі

Таким чином, після замкнення об’єкта зворотним зв’язком з матрицей коефіцієнтів отримано стійку систему, в якій характеристики перехідного процеса відповідають заданим вимогам.

СПИСОК ЛІТЕРАТУРИ

1. Бесекерский В.А. Теория автоматического регулирования / В.А. Бесекерский, Е.П. Попов. – М.: Наука, Главная редакция физ.-мат. литературы, 1975. – 768 с.

2. Андреев Ю.Н. Управление конечномерными линейными объектами / Ю.Н. Андреев. – М.: Наука, 1976. – 424 с.

3. Воронов А.А. Введение в динамику сложных управляемых систем / А.А. Воронов. – М.: Наука, 1985. – 352 с.

4. Медведев В.С. Control System Toolbox. MATLAB 5 для студентов / В.С. Медведев, В.Г. Потемкин. – М.: ДИАЛОГ-МИФИ, 1999. – 287 с.

5. Андриевский Б.Р. Избранные главы теории автоматического управления с примерами на языке MATLAB / Б.Р. Андриевский, А.Л. Фрадков. – СПб: Наука, 1999. – 475 с.

6. Григорьев В.В. Синтез систем автоматического управления методом модального управления / В.В. Григорьев, Н.В. Журавлёва, Г.В. Лукьянова, К.А. Сергеев. – СПб: СПбГУ ИТМО, 2007. – 108 с.

ЗМІСТ

ВСТУП . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1. Математичні моделі лінійних динамічних систем . . . . . . . . . . . . . . . 4

1.2. Часові характеристики лінійних динамічних систем . . . . . . . . . . . . . 7

1.3. Чаcтотні характеристики лінійних динамічних систем . . . . . . . . . . . . 9

1.4. Оформлення графіків в MATLAB . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

1.5. Задача модального керування . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

2. ВАРІАНТИ РОЗРАХУНКОВОГО ЗАВДАННЯ . . . . . . . . . . . . . . . . . . . . . 16

3. ПРИКЛАД ВИКОНАННЯ РОЗРАХУНКОВОГО ЗАВДАННЯ . . . . . . . . . 35

СПИСОК ЛІТЕРАТУРИ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

Навчальне видання

МЕТОДИЧНІ ВКАЗІВКИ

до виконання розрахункового завдання

«Побудова математичних моделей динамічних систем

та розв’язання задачі модального керування»

з курсу «Теорія керування»

для студентів напрямків 6.040301 «Прикладна математика»,

6.040302 «Інформатика» та 6.040303 «Системний аналіз»

У к л а д а ч і:

ДОРОФЄЄВ Юрій Іванович

КОСТЮК Ольга Василівна

Відповідальний за випуск О.С. Куценко

Роботу до видання рекомендував М.І. Безменов

В авторській редакції

План 2012, поз.

Підп. до друку Формат 60×84 1/16. Папір офісний.

Riso-друк. Гарнітура Таймс. Ум. друк. арк.0,7

Наклад 50 прим. Зам. № Ціна договірна

Видавець і виготовлювач

Видавничий центр НТУ «ХПІ»,

вул. Фрунзе, 21, м. Харків, 61002

Свідоцтво суб’єкта видавничої справи ДК № 3657 від 24.12.2009 р.

[1] На сірому фоні наводяться відповіді середовища MATLAB.

⇐ Предыдущая 1 2 3 4 56