Главная | Обратная связь

Распространение выборочных результатов на генеральную совокупность

Конечной целью выборочного наблюдения является характеристика генеральной совокупности. При малых объемах выборки эмпирические оценки параметров ( и 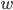) могут существенно отклоняться от их истинных значений ( и ). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров ( и 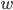) лежат истинные значения ( и ).

Доверительным интерваломкакого-либо параметра θгенеральной совокупности называется случайная область значений этого параметра, которая с вероятностью близкой к 1 (надежностью) содержит истинное значение этого параметра.

Предельная ошибка выборки Δпозволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы, которые равны:

Нижняя граница доверительного интервала получена путем вычитания предельной ошибки из выборочного среднего (доли), а верхняя — путем ее добавления.

Доверительный интервал для средней использует предельную ошибку выборки и для заданного уровня достоверности определяется по формуле:

Это означает, что с заданной вероятностью Р, которая называется доверительным уровнем и однозначно определяется значением t, можно утверждать, что истинное значение средней лежит в пределах от ,а истинное значение доли 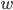— в пределах от

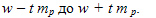
При расчете доверительного интервала для трех стандартных доверительных уровней Р = 95%, Р = 99% и Р = 99,9% значение 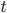выбирается по таблице Стьюдента. Приложения в зависимости от числа степеней свободы . Если объем выборки достаточно велик, то соответствующие этим вероятностям значения t равны: 1,96, 2,58 и 3,29. Таким образом, предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

Распространение результатов выборочного наблюдения на генеральную совокупность в социально-экономических исследованиях имеет свои особенности, так как требует полноты представительности всех ее типов и групп. Основой для возможности такого распространения является расчет относительной ошибки:

где Δ_%- относительная предельная ошибка выборки; , .

Существуют два основных метода распространения выборочного наблюдения на генеральную совокупность: прямой пересчет и способ коэффициентов.

Сущность прямого пересчетазаключается в умножении выборочного среднего значения !!\overline{x} на объем генеральной совокупности .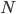

Пример. Пусть среднее число детей ясельного возраста в городе оценено выборочным методом и составило 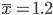человека. Если в городе 1000 молодых семей, то число необходимых мест в муниципальных детских яслях получают умножением этой средней на численность генеральной совокупности N = 1000, т.е. составит 1200 мест.

Способ коэффициентов целесообразно использовать в случае, когда выборочное наблюдение проводится с целью уточнения данных сплошного наблюдения.

При этом используют формулу:

,

где все переменные — это численность совокупности:

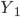— с поправкой на недоучет,

- без этой поправки,

— в контрольных точках

— в тех же точках по данным контрольных мероприятий.