Главная | Обратная связь

Основные характеристики параметров генеральной и выборочной совокупности

В основе статистических выводов проведенного исследования лежит распределение случайной величины , наблюдаемые же значения (х₁, х₂, … , х_n) называются реализациями случайной величины Х (n — объем выборки). Распределение случайной величины в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции распределения в каждой точке пространства возможных значений случайной величины . Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожидание и дисперсия .

По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное. Выборочными аналогами параметров и для него являются: среднее значение и эмпирическая дисперсия . Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком (она обозначена буквой ); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p). Дисперсия же альтернативного распределения также имеет эмпирический аналог .

В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения. Основные из них для теоретического и эмпирического распределений приведены в табл. 9.1.

Долей выборки k_n называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

k_n = n/N.

Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n:

w = n_n/n.

Пример. В партии товара, содержащей 1000 ед., при 5% выборке доля выборки k_n в абсолютной величине составляет 50 ед. (n = N*0,05); если же в этой выборке обнаружено 2 бракованных изделия, то выборочная доля брака w составит 0,04 (w = 2/50 = 0,04 или 4%).

Так как выборочная совокупность отлична от генеральной, то возникают ошибки выборки.

Таблица 9.1 Основные параметры генеральной и выборочной совокупностей

Ошибки выборки

При любом статистическом наблюдении (сплошном и выборочном) могут встретиться ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный и систематический характер. Случайные ошибки складываются из множества различных неконтролируемых причин, носят непреднамеренный характер и обычно по совокупности уравновешивают друг друга (например, изменения показателей прибора при температурных колебаниях в помещении).

Систематические ошибки тенденциозны, так как нарушают правила отбора объектов в выборку (например, отклонения в измерениях при изменении настройки измерительного прибора).

Пример. Для оценки социального положения населения в городе предусмотрено обследовать 25% семей. Если при этом выбор каждой четвертой квартиры основан на ее номере, то существует опасность отобрать все квартиры только одного типа (например, однокомнатные), что обеспечит систематическую ошибку и исказит результаты; выбор же номера квартиры по жребию более предпочтителен, так как ошибка будет случайной.

Ошибки репрезентативности присущи только выборочному наблюдению, их невозможно избежать и они возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Значения показателей, получаемых по выборке, отличаются от показателей этих же величин в генеральной совокупности (или получаемых при сплошном наблюдении).

Ошибка выборочного наблюдения есть разность между значением параметра в генеральной совокупности и ее выборочным значением. Для среднего значения количественного признака она равна: , а для доли (альтернативного признака) — .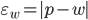

Ошибки выборки свойственны только выборочным наблюдениям. Чем больше эти ошибки, тем больше эмпирическое распределение отличается от теоретического. Параметры эмпирического распределения и являются случайными величинами, следовательно, ошибки выборки также являются случайными величинами, могут принимать для разных выборок разные значения и поэтому принято вычислять среднюю ошибку.

Средняя ошибка выборкиесть величина , выражающая среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении принципа случайного отбора зависит прежде всего от объема выборки 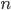и от степени варьирования признака: чем больше 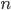и чем меньше вариация признака (следовательно, и значение ), тем меньше величина средней ошибки выборки . Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:

т.е. при достаточно больших 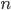можно считать, что . Средняя ошибка выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной. В табл. 9.2 приведены выражения для вычисления средней ошибки выборки при разных методах организации наблюдения.

Таблица 9.2 Средняя ошибка (m) выборочных средней и доли для разных видов выборки

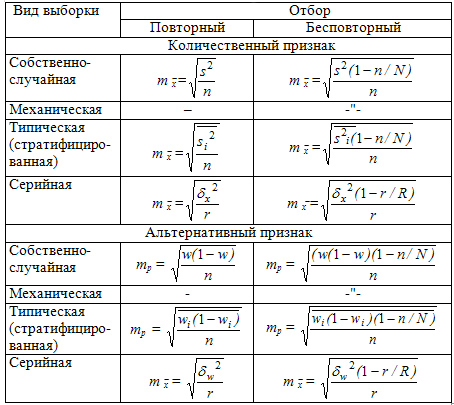
Где - средняя из внутригрупповых выборочных дисперсий для непрерывного признака;

- средняя из внутригрупповых дисперсий доли;

— число отобранных серий, — общее число серий;

,

где — средняя -й серии;

— общая средняя по всей выборочной совокупности для непрерывного признака;

,

где — доля признака в -й серии;

— общая доля признака по всей выборочной совокупности.

Однако о величине средней ошибки можно судить лишь с определенной, вероятностью Р (Р ≤ 1). Ляпунов А.М. доказал, что распределение выборочных средних , a следовательно, и их отклонений от генеральной средней, при достаточно большом числе 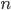приближенно подчиняется нормальному закону распределения при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.

Математически это утверждение для средней выражается в виде:

а для доли выражение (1) примет вид:

где -естьпредельная ошибка выборки, которая кратна величине средней ошибки выборки , а коэффициент кратности 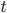— есть критерий Стьюдента ("коэффициент доверия"), предложенный У.С. Госсетом (псевдоним "Student"); значения 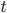для разного объема выборки 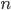хранятся в специальной таблице.

Значения функции Ф(t) при некоторых значениях t равны:

Следовательно, выражение (3) может быть прочитано так: с вероятностью Р = 0,683 (68,3%) можно утверждать, что разность между выборочной и генеральной средней не превысит одной величины средней ошибкиm (t = 1), с вероятностью Р = 0,954 (95,4%) — что она не превысит величины двух средних ошибокm (t = 2) , с вероятностью Р = 0,997 (99,7%) — не превысит трех значений m (t = 3) .Таким образом, вероятность того, что эта разность превысит трехкратную величину средней ошибки определяет уровень ошибки и составляет не более 0,3%.

В табл. 9.3 приведены формулы для вычисления предельной ошибки выборки.

Таблица 9.3 Предельная ошибка (D) выборки для средней и доли (р) для разных видов выборочного наблюдения