 |
|
Теоретичні відомості
Для геометричного опису полів вводять поняття ліній напруженості. Їх проводять так, щоб дотична до них у кожній точці збігалася з напрямком вектора напруженості, а густота ліній, тобто число ліній, що пронизують одиничну площадку, перпендикулярну лініям у даній точці, була б пропорційна модулю вектора напруженості. Крім того, цим лініям приписують напрямок, що збігається з напрямком вектора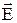 
. По отриманій картині можна легко визначити конфігурацію даного електричного поля, тобто знайти напрямок і модуль вектора 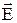в різних точках поля. Якщо густота ліній у будь–якій точці стала, то поле називають однорідним. Потоком ліній напруженості називають число ліній, що пронизують елементарну площадку dS, нормаль до якої складає кут a з вектором напруженості:
,
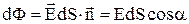Якщо мається деяка довільна поверхня S, то потік вектора 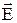крізь неї:
.
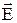Ця величина алгебраїчна: вона залежить не тільки від конфігурації поля , але і від вибору напрямку нормалі. У випадку замкнених поверхонь прийнято нормаль 
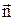брати назовні області, що охоплюється цими поверхнями, тобто вибирати зовнішню нормаль.
Теорема Гаусса: Потік вектора 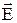крізь замкнуту поверхню дорівнює відношенню алгебраїчної суми зарядів усередині цієї поверхні до електричній сталій e0:
.
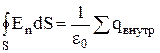З теореми Гаусса випливає, що при будь–якому переміщенні зарядів усередині поверхні потік ліній напруженості через межу поверхні не змінюється.
Теорема Гаусса в диференціальній формі. Нехай заряд q розподілений в об’ємі V, який охоплюється замкнутою поверхнею S, із середньою об'ємною густиною 
. Тоді можна записати:
.
Підставимо цю формулу в математичне вираження теореми Гаусса і розділимо обидві частини отриманого рівняння на V. У результаті одержимо:
.
Визначимо напруженість у центрі виділеного об’єму. Для цього спрямуємо об’єм V до нуля, стягаючи його до цікавлячій нас точці поля. При цьому середня густина буде наближатись до густини r в даній точці поля, тобто:
.
Величину, що є межею відношення 
до V при V ® 0, називають дивергенцією поля 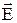и позначають dіv :
.
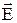Після відповідної заміни теорема Гаусса приймає вигляд:
.
Отримане вираження називається теоремою Гаусса в диференціальній формі.
У декартовій системі координат вектор 
можна представити в наступному вигляді:
.
Введемо векторний диференціальний оператор набла:
.
Помножимо скалярно вектор набла на вектор напруженості:
.
Тоді теорема Гаусса в диференціальній формі приймає вигляд:
.
У диференціальній формі теорема Гаусса є локальною теоремою: дивергенція поля напруженості в даній точці залежить тільки від густини електричного заряду в тій же точці.