 |
|
Теоретичні відомості
У 1820 р. датський фізик Ерстед помітив, що магнітна стрілка, розміщена поблизу провідника з струмом, відхиляється від початкового стану. Дослідження показали, що стрілка повертається і намагається розміститися так, щоб її вісь була перпендикулярна до провідника. Із зміною напряму струму змінюється і напрям повертання магнітної стрілки. Пізніші дослідження показали, що навколо будь-якого електричного струму, тобто рухомої зарядженої частинки, нерозривно існує магнітне поле, яке виявляється за впливом на магнітну стрілку. Магнітне поле – це вид матерії, за допомогою якої взаємодіють електричні заряди, що рухаються. Воно виявляється за дією на магнітну стрілку або провідник із струмом.
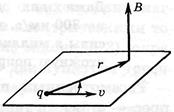 Силовою характеристикою магнітного поля в кожній точці є вектор магнітної індукції
Силовою характеристикою магнітного поля в кожній точці є вектор магнітної індукції 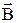 . Напрям і величину вектора індукції визначають за дією магнітного поля на магнітну стрілку та провідник із струмом. За напрям вектора магнітної індукції в заданій точці поля приймають напрям вектора сили, з якою поле діє на північний полюс нескінченно малої магнітної стрілки, розміщеної в цій точці. Для графічного зображення магнітного поля користуються лініями магнітної індукції. Лініями магнітної індукціїназивають криві, дотичні до яких у кожній точці збігаються з напрямом вектора
. Напрям і величину вектора індукції визначають за дією магнітного поля на магнітну стрілку та провідник із струмом. За напрям вектора магнітної індукції в заданій точці поля приймають напрям вектора сили, з якою поле діє на північний полюс нескінченно малої магнітної стрілки, розміщеної в цій точці. Для графічного зображення магнітного поля користуються лініями магнітної індукції. Лініями магнітної індукціїназивають криві, дотичні до яких у кожній точці збігаються з напрямом вектора 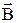 в цих точках поля. Лінії магнітної індукції завжди замкнуті й охоплюють провідник із струмом. Для визначення напряму ліній магнітної індукції користуються правилом свердлика: якщо свердлик повертати так, щоб його поступальний рух збігався з напрямом струму І, то обертальний рух рукоятки покаже напрям ліній магнітної індукції. У відмінності від електричного поля, яке діє як на нерухомі, так і на рухомі заряди, магнітне поле діє тільки на заряди, що рухаються. Напрямок і модуль магнітної сили залежить від швидкості заряду, його величини і вектора магнітної індукції в даній точці:
в цих точках поля. Лінії магнітної індукції завжди замкнуті й охоплюють провідник із струмом. Для визначення напряму ліній магнітної індукції користуються правилом свердлика: якщо свердлик повертати так, щоб його поступальний рух збігався з напрямом струму І, то обертальний рух рукоятки покаже напрям ліній магнітної індукції. У відмінності від електричного поля, яке діє як на нерухомі, так і на рухомі заряди, магнітне поле діє тільки на заряди, що рухаються. Напрямок і модуль магнітної сили залежить від швидкості заряду, його величини і вектора магнітної індукції в даній точці:
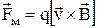 .
.
Повна електромагнітна сила, що діє на заряд q із сторони електромагнітного поля, визначається за формулою:
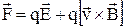 .
.
Її називають силою Лоренца. Слід відзначити, що напрямок магнітної сили завжди перпендикулярний швидкості руху зарядів, отже магнітна сила роботи не виконує. У результаті узагальнення експериментальних даних був отриманий експериментальний закон, який визначає магнітну індукцію поля точкового заряду q, що рухається з постійною швидкістю 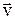 :
:
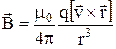 ,
,
де m0 – магнітна стала (m0 = 4p*10–7Гн/м), 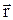 – радіус–вектор, що спрямований від заряда q до точки спостереження.
– радіус–вектор, що спрямований від заряда q до точки спостереження.
Кінець радіус–вектора нерухомий у даній системі відліку, а початок рухається із швидкістю 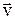 , тому вектор
, тому вектор 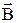 залежить не тільки від точки спостереження, а і від часу. Вектору
залежить не тільки від точки спостереження, а і від часу. Вектору 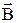 спрямований перпендикулярно до плоскості, в який знаходяться вектори
спрямований перпендикулярно до плоскості, в який знаходяться вектори 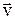 і
і 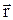 , до того ж обертання від вектора
, до того ж обертання від вектора 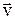 до
до 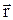 і вектор
і вектор 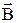 утворюють правогвинтову систему. Одиницею вимірювання магнітної індукції в СІ служить Тесла [Тл]. Знайдемо зв’язок між напруженість електричного поля і індукцією магнітного поля. Напруженість електричного поля, що створюється електричним зарядом:
утворюють правогвинтову систему. Одиницею вимірювання магнітної індукції в СІ служить Тесла [Тл]. Знайдемо зв’язок між напруженість електричного поля і індукцією магнітного поля. Напруженість електричного поля, що створюється електричним зарядом:
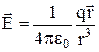 .
.
Тоді формулу для 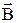 можна записати у вигляді:
можна записати у вигляді:
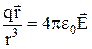 ,
, 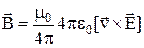 ,
,  .
.
Якщо увести сталу:
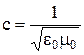 ,
,
то остання формула приймає вигляд:
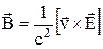 ,
,
де с – електродинамічна стала.
Визначимо магнітну індукцію сукупності зарядів, що рухаються. Якщо об’ємна густина зарядів r, то заряд в елементарному об’ємі dV:
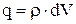 .
.
Враховуючи, що 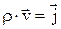 , формулу магнітної індукції поля елементу із струмом можна записати у вигляді:
, формулу магнітної індукції поля елементу із струмом можна записати у вигляді:

або
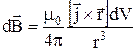 .
.
Отримана формула є математичним виразом закону Біо–Савара–Лапласа. Отримаємо цей закон в іншому вигляді. Якщо струм тече по тонкому провіднику з площею поперечного перерізу dS, то
 ,
,
де dl – елемент довжини проводу.
У векторному вигляді:
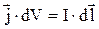 ,
,
де 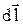 – вектор у напрямку струму.
– вектор у напрямку струму.
Тоді формула магнітної індукції поля елементу із струмом приймає вигляд:
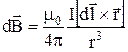 .
.
Для магнітного поля справедливий принцип суперпозиції, у відповідності з яким магнітна індукція результуючого поля дорівнює геометричній сумі індукцій елементарних струмів:
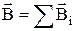 .
.
Для індукції результуючого поля закон Біо–Савара–Лапласа має вигляд:
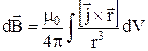
або
 .
.
Як відомо, електричний струм являє собою упорядкований рух електричних зарядів, на які із сторони магнітного поля діє магнітна сила. Сила, яка діє на сукупність зарядів, які упорядковано рухаються, тобто на струм, називається силою Ампера.
Нехай об’ємна густина зарядів, що упорядковано рухаються, дорівнює r. Заряд, який знаходиться у елементарному об’ємі dV дорівнює 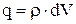 . Тоді сила, яка діє на елемент із струмом dV може бути знайдена за формулою:
. Тоді сила, яка діє на елемент із струмом dV може бути знайдена за формулою:
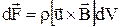 , (1)
, (1)
де 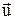 – середня швидкість упорядкованого руху зарядів.
– середня швидкість упорядкованого руху зарядів.
Так як густина струму  , то після відповідної заміни отримуємо:
, то після відповідної заміни отримуємо:
 .
.
Якщо струм тече по тонкому провіднику, то у відповідності з визначенням густини струму
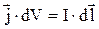
і формула (1) приймає остаточний вигляд:
 , (2)
, (2)
де 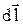 – вектор, який співпадає за напрямком зі струмом і характеризує елемент довжини тонкого провідника.
– вектор, який співпадає за напрямком зі струмом і характеризує елемент довжини тонкого провідника.
Рівняння (2) являє собою математичний вираз закону Ампера. За модулем формула (2) записується так:
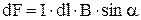 ,
,
де a – кут між векторами 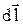 і
і 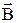 .
.
Закон Ампера: Сила, яка діє на прямолінійний провідник із струмом, що перебуває в однорідному магнітному полі, прямо пропорційна силі струму, довжині провідника, магнітній індукції і синусові кута між напрямом струму і вектором 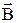 . Напрям сили Ампера визначається за правилом правого гвинта.
. Напрям сили Ампера визначається за правилом правого гвинта.
Якщо у магнітному полі знаходиться замкнений контур зі струмом то формула закону Ампера має вигляд:
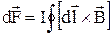 .
.
Із останньої формули випливає, що в однорідному магнітному полі 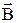 виноситься із під інтегралу, а інтеграл
виноситься із під інтегралу, а інтеграл  , отже
, отже 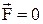 . Якщо поле неоднорідне, то сила розраховується у кожному випадку за законом Ампера.
. Якщо поле неоднорідне, то сила розраховується у кожному випадку за законом Ампера.
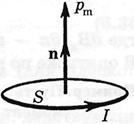 Розглянемо плоский контур, який знаходиться у неоднорідному магнітному полі. Якщо його розміри достатньо малі, то контур називається елементарним. Для опису поведінки елементарного контуру у магнітному полі вводять вектор магнітного моменту. Це вектор, який визначається із виразу:
Розглянемо плоский контур, який знаходиться у неоднорідному магнітному полі. Якщо його розміри достатньо малі, то контур називається елементарним. Для опису поведінки елементарного контуру у магнітному полі вводять вектор магнітного моменту. Це вектор, який визначається із виразу:
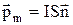 ,
,
де I – сила струму, S – площа контуру, 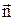 – вектор нормалі, напрямок якого зв’язаний з напрямком струму правилом правого гвинта.
– вектор нормалі, напрямок якого зв’язаний з напрямком струму правилом правого гвинта.
Розрахунки показують, що сила, яка діє на елементарний контур зі струмом, що знаходиться в неоднорідному магнітному полі, визначається за формулою:
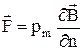 , (3)
, (3)
де pm – модуль магнітного моменту контуру, 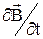 – перша похідна вектору
– перша похідна вектору 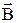 за напрямком нормалі
за напрямком нормалі 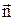 .
.
Із формули (3) випливає:
- у однорідному магнітному полі 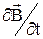 = 0 і
= 0 і 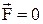 ;
;
- напрямок вектора сили не співпадає ні з вектором 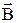 , ні з вектором
, ні з вектором 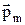 , а співпадає тільки напрямком елементарного приросту вектору
, а співпадає тільки напрямком елементарного приросту вектору 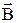 , який узятий у напрямку вектору
, який узятий у напрямку вектору 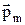 у місті розташування контуру.
у місті розташування контуру.
Момент сил, який діє на контур із струмом. Розглянемо плоский контур із струмом I, який знаходиться в однорідному магнітному полі. Результуюча сила Ампера, що діє на нього, дорівнює нулю. Із курсу механіки відомо, що у цьому випадку сумарний момент сил не залежить від точки О, відносно якої визначають моменти цих сил. За визначенням, результуючий момент сил Ампера:
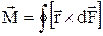 (4)
(4)
Розрахунки показують, що для контуру із струмом довільної форми момент сил можна представити наступним чином:
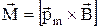 (5)
(5)
Із формули (5) випливає, що в однорідному магнітному полі вектор моменту сил Ампера, які діють контур із струмом, перпендикулярний як вектору 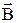 , так і вектору
, так і вектору 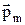 . Модуль вектору
. Модуль вектору  визначається за виразом:
визначається за виразом:
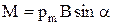 ,
,
де a – кут між векторами 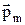 і
і 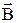 .
.
Слід відзначити, що формула (5) справедлива і для неоднорідного поля, але якщо розміри контуру із струмом досить малі.
Робота при переміщенні контуру із струмом у магнітному полі. Розглянемо випадок, коли контур з рухливою перемичкою довжини l знаходиться в однорідному магнітному полі, яке перпендикулярно площині контуру і спрямовано за площину малюнка. На перемичку діє сила Ампера:

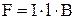 .
.
При переміщенні перемички вправо на dx ця сила виконує позитивну роботу
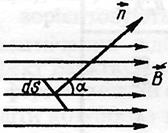
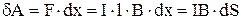 ,
,
де dS – збільшення площі, обмеженої контуром.
Магнітним потоком називають скалярну фізичну величину, яка дорівнює кількості ліній магнітної індукції, що пронизують контур, і яка визначається за формулою:
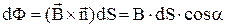 ,
,
де a – кут між векторами 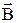 і
і 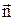 .
.
Одиниці магнітного потоку у СІ:
[Вб]. 1Вб = 1Тл*1м2.
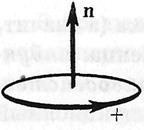
Для визначення знака магнітного потоку dФ умовимося завжди брати нормаль 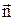 до поверхні, яка обмежена контуром, так, щоб вона утворювала з напрямком струму в контурі правогвинтову систему. При цьому струм I буде завжди величиною позитивною. Потік же може бути як позитивним, так і негативним. З урахуванням останнього визначення формула роботи приймає вигляд:
до поверхні, яка обмежена контуром, так, щоб вона утворювала з напрямком струму в контурі правогвинтову систему. При цьому струм I буде завжди величиною позитивною. Потік же може бути як позитивним, так і негативним. З урахуванням останнього визначення формула роботи приймає вигляд:
 .
.
Робота сил Ампера при повному переміщенні контуру з положення 1 у положення 2 визначається із виразу:
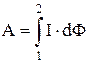 .
.
Якщо струм не змінюється, то:
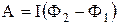 ,
,
де Ф1 та Ф2 – магнітні потоки скрізь контур у початковому та кінцевому положеннях.
У 1831 р. М. Фарадей відкрив явище електромагнітної індукції, яке полягає в тім, що в замкнутому провідному контурі при зміні магнітного потоку, охоплюваного цим контуром, виникає електричний струм – його назвали індукційним. Поява індукційного струму означає, що при зміні магнітного потоку в контурі виникає е.р.с. індукції ei. При цьому було встановлено, що величина ei не залежить від того, яким чином здійснюється зміна магнітного потоку Ф, а визначається лише швидкістю його зміни, тобто величиною 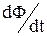 . Крим того, зміна знака похідної
. Крим того, зміна знака похідної 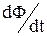 приводить до зміни знака або «напрямку» ei. Напрямок індукційного струму визначається правилом Ленца:індукційний струм завжди спрямований так, щоб протидіяти причині, яка його зухвалює. Інакше кажучи, індукційний струм створює магнітний потік, що перешкоджає зміні магнітного потоку, що викликає е.р.с. індукції.
приводить до зміни знака або «напрямку» ei. Напрямок індукційного струму визначається правилом Ленца:індукційний струм завжди спрямований так, щоб протидіяти причині, яка його зухвалює. Інакше кажучи, індукційний струм створює магнітний потік, що перешкоджає зміні магнітного потоку, що викликає е.р.с. індукції.
 Явище електромагнітної індукції покладено в основу закону електромагнітної індукції:Е.Р.С. індукції, яка виникає в замкнутому контурі, що знаходиться в магнітному полі, прямо пропорційна швидкості зміни магнітного потоку, що пронизує контур:
Явище електромагнітної індукції покладено в основу закону електромагнітної індукції:Е.Р.С. індукції, яка виникає в замкнутому контурі, що знаходиться в магнітному полі, прямо пропорційна швидкості зміни магнітного потоку, що пронизує контур:
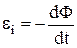 .
.
Знак мінус у цьому рівнянні зв'язаний з правилом знаків. Оскільки магнітний потік визначається за формулою 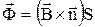 , його враховують позитивним, якщо він співпадає з вектором
, його враховують позитивним, якщо він співпадає з вектором 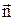 до контуру, при цьому вектор нормалі і позитивний напрямок обходу зв’язані один з іншим правилом правого гвинта. Знак
до контуру, при цьому вектор нормалі і позитивний напрямок обходу зв’язані один з іншим правилом правого гвинта. Знак 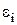 зв’язаний з вектором зміни магнітного потоку. Якщо замкнутий контур, у якому індуцірується е.р.с., складається не з одного витка, а з N витків, то
зв’язаний з вектором зміни магнітного потоку. Якщо замкнутий контур, у якому індуцірується е.р.с., складається не з одного витка, а з N витків, то 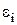 буде дорівнює сумі е.р.с, що індуціруються у кожнім з витків. І якщо магнітний потік, охоплюваний кожним витком, однаковий і дорівнює Ф1, то сумарний потік Ф крізь поверхню, натягнуту на такий складний контур, можна представити як:
буде дорівнює сумі е.р.с, що індуціруються у кожнім з витків. І якщо магнітний потік, охоплюваний кожним витком, однаковий і дорівнює Ф1, то сумарний потік Ф крізь поверхню, натягнуту на такий складний контур, можна представити як:
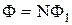 .
.
Цю величину називають повним магнітним потоком або потокозчепленням. У цьому випадку відповідна э.р.с. індукції в контурі визначається згідно формулою
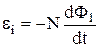 .
.
Природа електромагнітної індукції. Розглянемо послідовно два випадки.
1. Контур рухається в постійному магнітному полі. Насамперед звернемося до контуру з рухливою перемичкою довжиною l. Нехай він знаходиться в однорідному магнітному полі, перпендикулярному площині контуру і спрямованому за площину малюнка. Почнемо рухати перемичку вправо зі швидкістю v. З такою же швидкістю почнуть рухатися і носії струму в перемичці – електрони. У результаті на кожен електрон почне діяти уздовж перемички магнітна сила  , і електрони почнуть переміщатися по перемичці вниз, тобто потече індукційний струм, спрямований нагору. Заряди, що перерозподілилися, створять електричне поле, що збудить струм і в інших ділянках контуру. Магнітна сила
, і електрони почнуть переміщатися по перемичці вниз, тобто потече індукційний струм, спрямований нагору. Заряди, що перерозподілилися, створять електричне поле, що збудить струм і в інших ділянках контуру. Магнітна сила 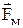 відіграє роль сторонньої сили. Оскільки
відіграє роль сторонньої сили. Оскільки
 ,
, 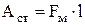 і
і 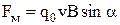 ,
,
то після відповідних замін отримаємо:
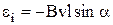 .
.
Знак мінус поставлений у зв'язку з правилом знаків: нормаль n до поверхні, натягнутої на наш контур, обираємо за площину рисунку, і тому за правилом правого гвинта позитивний напрямок обходу контуру – по годинній стрілці. При цьому стороннє поле 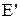 спрямоване проти позитивного напрямку обходу контуру і
спрямоване проти позитивного напрямку обходу контуру і  – величина негативна. Добуток vl у формулі е.р.с. є збільшення площі, обмеженої контуром, в одиницю часу
– величина негативна. Добуток vl у формулі е.р.с. є збільшення площі, обмеженої контуром, в одиницю часу 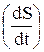 , тому
, тому
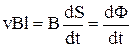 ,
,
де dФ – збільшення магнітного потоку крізь площу контуру.
Таким чином,
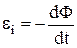 .
.
Можна в загальному виді довести, що закон електромагнітної індукції справедливий для будь-якого контуру, що рухається довільним образом у постійному неоднорідному магнітному. Отже, виникнення е.р.с. індукції при русі контуру в постійному магнітному полі обумовлене дією магнітної сили, що діє на заряди в провіднику при його русі.
2. Контур не рухається в перемінному магнітному полі. Виникнення індукційного струму і у цьому випадку свідчить про те, що магнітне поле, яке змінюється з часом, викликає в контурі появу сторонніх сил. Максвелл припустив, що в цьому випадку в просторі виникає електричне поля незалежно від наявності провідного контуру. Останній лише дозволяє знайти по виникненню в ньому індукційного струму існування цього електричного поля. Таким чином, відповідно до Максвелла магнітне поле, що змінюється з часом, породжує електричне поле. Циркуляція вектора напруженості цього поля по будь-якому нерухомому контуру визначається як
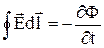 .
.
Тут символ частинної похідної за часом  підкреслює той факт, що контур і натягнута на нього поверхня нерухомі. Оскільки потік
підкреслює той факт, що контур і натягнута на нього поверхня нерухомі. Оскільки потік
 ,
,
то
 і
і 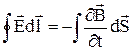 .
.
Із отриманого рівняння свідчить, що циркуляція вектора напруженості 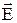 , що збуджується змінним магнітним полем, відмінна від нуля. Це означає, що електричне поле не потенційно, воно, як і магнітне поле, є вихровим.
, що збуджується змінним магнітним полем, відмінна від нуля. Це означає, що електричне поле не потенційно, воно, як і магнітне поле, є вихровим.
Висновок: При буд якій зміні магнітного поля у просторі виникає вихрове електричне поле, яке у замкненому контурі, що знаходиться в даній точці простору, збуджує індукційний струм.
Явище самоіндукції. Електромагнітна індукція виникає у всіх випадках, коли змінюється магнітний потік крізь контур. При цьому зовсім не важливо, чим викликається ця зміна потоку. Якщо в деякому контурі тече струм, що змінюється в часі, то магнітне поле цього струму також буде змінюватися. Це спричиняє зміну магнітного потоку через контур, а отже, і появу е.р.с. індукції. Таким чином, зміна струму в контурі веде до виникнення е.р.с. індукції в цьому ж самому контурі. Дане явище називають самоіндукцією. Якщо в просторі, де знаходиться контур зі струмом, немає феромагнетиків, поле вектора 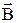 , а виходить, і повний магнітний потік Ф через контур будуть пропорційні силі струму (Ф~I), і можна записати:
, а виходить, і повний магнітний потік Ф через контур будуть пропорційні силі струму (Ф~I), і можна записати:
 ,
,
де L – коефіцієнт, називанийіндуктивністюконтуру.
Індуктивність L залежить від форми і розмірів контуру, а також від магнітних властивостей навколишнього середовища. Якщо контур твердий і поблизу від нього немає феромагнетиків, індуктивність є величиною постійною, що не залежить від сили струму. Одиницею індуктивності є Генрі (Гн). Індуктивністю 1 Гн володіє контур, магнітний потік крізь який при струмі 1 А дорівнює 1 Вб. 1 Гн = 1 Вб/А.
Е.Р.С. самоіндукції з урахуванням індуктивності можна представити наступним чином:
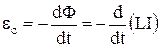 .
.
Якщо індуктивність контуру не змінюється, то
 .
.
Знак мінус показує, що 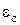 завжди спрямована так, щоб перешкоджати зміні сили струму. Ця е.р.с. прагне зберегти струм незмінним: вона протидіє току, коли він збільшується, і підтримує струм, коли він зменшується. У явищах самоіндукції струм володіє "інерцією", тому що ефекти індукції прагнуть зберегти магнітний потік постійним, точно так само, як механічна інерція прагне зберегти швидкість тіла незмінною.
завжди спрямована так, щоб перешкоджати зміні сили струму. Ця е.р.с. прагне зберегти струм незмінним: вона протидіє току, коли він збільшується, і підтримує струм, коли він зменшується. У явищах самоіндукції струм володіє "інерцією", тому що ефекти індукції прагнуть зберегти магнітний потік постійним, точно так само, як механічна інерція прагне зберегти швидкість тіла незмінною.
Енергія магнітного поля струму. Замкнемо нерухоме електричне коло, що містить індуктивність L і опір R, на джерело струму з е.р.с. 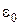 . У контурі почне зростати струм. Це приводить до появи е.р.с. самоіндукції
. У контурі почне зростати струм. Це приводить до появи е.р.с. самоіндукції 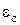 . Відповідно до закону Ома
. Відповідно до закону Ома 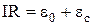 , відкіля
, відкіля 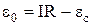 . Знайдемо елементарну роботу, яку виконують сторонні сили за час dt. Для цього помножимо попередню рівність на Іdt:
. Знайдемо елементарну роботу, яку виконують сторонні сили за час dt. Для цього помножимо попередню рівність на Іdt:
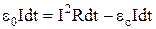 .
.
З огляду на зміст кожного доданка і співвідношення 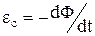 , запишемо:
, запишемо:
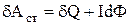 .
.
З отриманого рівняння свідчить, що в процесі встановлення струму, коли потік Ф міняється і dФ> 0, робота, яку виконує джерело, виявляється більше виділюваної в колі джоулевої теплоти. Частина цієї роботи відбувається проти е.р.с. самоіндукції. Після того як струм установиться, dФ = 0 і вся робота джерела буде іти тільки на виділення джоулевої теплоти. Отже, додаткова робота, чинена сторонніми силами проти е.р.с. самоіндукції в процесі встановлення
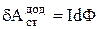 .
.
Оскільки при відсутності феромагнетику 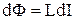 , то отримуємо:
, то отримуємо:
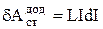 .
.
Проінтегрував це рівняння при зміні струму від нуля до I, одержимо:
 .
.
За законом збереження енергії будь-яка робота йде на збільшення якогось виду енергії. Частина роботи сторонніх сил йде на збільшення внутрішньої енергії провідників, а інша частина – у процесі встановлення струму – на виникнення магнітного поля. Таким чином, можна зробити висновок, що при відсутності феромагнетиків контур з індуктивністю L, по якому тече струм I, має енергію 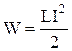 , яку називають енергією магнітного поля струму.
, яку називають енергією магнітного поля струму.
Енергія магнітного поля довгого соленоїда із струмом. Соленоїд – це одношарова котушка довжиною l площею перерізу S.
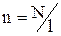 – число ампер витків, тобто число витків на одиницю довжини соленоїда. Визначимо індуктивність соленоїда. Оскільки
– число ампер витків, тобто число витків на одиницю довжини соленоїда. Визначимо індуктивність соленоїда. Оскільки  ,
, 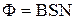 і
і 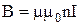 , то отримаємо:
, то отримаємо:
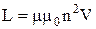 ,
,
де  – об’єм соленоїда.
– об’єм соленоїда.
Підставимо отриманий вираз у формулу енергії магнітного поля:
 .
.
За теоремою про циркуляцію вектора напруженості магнітного поля можна записати:
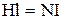
або
 .
.
Зробивши заміну в формулі енергії магнітного поля, отримуємо:
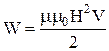 .
.
Враховуючи, що 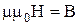 , можна записати:
, можна записати:
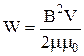
або
 .
.
Об’ємною густиною енергії магнітного поля називають енергію одиниці об’єму простору:
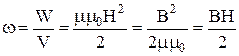 .
.