 |
|
Геометричні ймовірності
В попередніх параграфах розглядались випробування із скінченною множиною наслідків. Однак не всяка реальна задача може бути зведена до цієї схеми, оскільки часто зустрічаються випробування, у яких множина наслідків нескінченна. При розв’язуванні деяких із подібних задач зручно застосовувати геометричну модель.
Нехай дано відрізок довжиною 
. Розділимо його навпіл (для однозначності точку поділу будемо відносити до лівої половини). Наугад кидається точка на цей відрізок. Можливі два випадки: “точка попала на ліву половину” – подія 
, “точка попала на праву половину” – подія 
. Оскільки точка кидається наугад, то доцільно вважати, що ці події рівноможливі, тоді ймовірність події 
, так само 
.
Розділимо тепер відрізок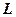 
на 10 рівних частин (довжина кожного 
). Випадковим чином кидають точку на цей відрізок. Можливі випадки: “точка попала на 1-й відрізок” – подія 
, “точка попала на 2-й відрізок” – подія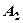 
, і т .д., “точка попала на 10-й відрізок” – подія 
. Вважаючи ці події рівноможливими, отримаємо, що ймовірність кожної з цих подій дорівнює 
, тобто
Нехай подія 
полягає в тому, що випадково кинута точка попала, наприклад на відрізок 
. Оскільки події сприяють чотири із можливих випадків, то ймовірність можна представити
,
(1)
- ймовірність випадкового попадання точки на відрізок довжиною 
, який міститься на відрізку довжиною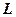 
.
Викладений підхід можна узагальнити для плоских фігур (див. рис. 1), а також у просторі для тіл.
Рис.1
Нехай фігура 
, площа якої дорівнює 
, міститься у фігурі 
, площа якої 
, тоді ймовірність події , яка полягає у тому, що наугад кинута точка попаде у фігуру , дорівнює відношенню площ цих фігур, тобто
. (2)
Для формул (1) і (2) мається на увазі “рівноможливість” випадкового попадання точки в довільну точку відповідно відрізка 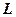чи фігури 
.
З метою наочності розглянемо таку модель.
Нехай фігура - це прямокутник розміру 
(його площа 
), описаний навколо фігури , нарисованої на асфальті. Замість точок, які навмання вибираються у прямокутнику, будемо вважати краплі дощу, що починається. Після певного часу накрапання прямокутник закривають від дощу і рахують кількість крапель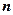 
, які попали у весь прямокутник , а також кількість крапель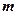 
, які попали у фігуру . Обчислимо відносну частоту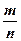 
. Нам вже відомо, що за формулою (2) можна знайти ймовірність події , яка полягає у випадковому виборі точки із фігури . У даному випадку це відношення площ 
, а з другого боку 
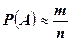. Тому маємо наближену рівність 
,
за допомогою якої можна знайти площу фігури ,
. (3)
Зрозуміло, що цей приклад наведено для наочності. У дійсності невідому площу за описаною ідеєю знаходять з застосуванням ЕОМ методом випадкового пошуку. Як це можна зробити, буде показано далі у задачі 2.
Розглянемо задачі.
Задача 1. Двоє студентів після занять домовились зустрітись біля виходу з корпуса. Оскільки у кожного з них могли з’явитись непередбачені справи, то зустріч домовились провести протягом години з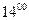 
до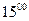 
. Таким чином, що перший, хто приходить до місця зустрічі, жде 15 хвилин (але не пізніше 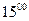) і йде собі. Знайти ймовірність зустрічі, якщо час очікування взяти: а) 15 хв; б) 20 хв; в) 30 хв.
Розв’язання. Нехай 
- час приходу першого студента на місце зустрічі,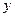 
- другого.
Зустріч відбувається за умови, щ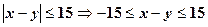о 
, або
Множина розв’язків нерівності зображена на рис 2.
Площа квадрата 
. Площа фігури 
. Тому ймовірність зустрічі (подія )
При 
хв. маємо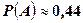 
; при 
хв. 
; при 
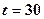хв. 
.
Рис. 2
Задача 2. Знайти площу параболічного сегмента заданого рівняннями 
і 
.
Розв’язання. Параболічний сегмент зображено на рис. 3.
Рис. 3
Точки перетину параболи з віссю 
і 
. Цю площу можна обчислити за допомогою визначеного інтеграла або за допомогою формули
,
де 
- коефіцієнт при 
у рівнянні параболи.
Покажемо, як знайти шукану площу, використовуючи геометричне означення ймовірності. Опишемо навколо параболічного сегмента квадрат із стороною 4 одиниці. Площа квадрата 
кв. од. (див. рис. 3). За допомогою стандартної функції генерування випадкових точок 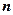, які попадають у квадрат, в тому числі 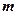точок, які у параболічному сегменті, знайдемо відносну частоту 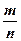попадання випадкових точок у параболічній сегмент. Тоді за формулою (3) знаходимо 
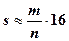. У таблиці 1 подані результати розрахунків наближених значень площі параболічного сегмента для різних значень 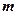і 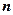. Так, з рис. 3 видно, що у квадрат попало 10 точок, а у сегмент – 6, тому для першого наближення площі маємо
;
що і записано у першому рядку таблиці 1.
Таблиця 1.
|
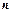
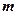
| Площа
|
| 9,6 | ||
| 10,56 | ||
| 1 000 | 10,32 | |
| 10 000 | 6 645 | 10,6336 |
| 100 000 | 66 865 | 10,6984 |
| 1000 000 | 666 727 | 10,6671 |
Із таблиці 1 видно, що із збільшенням 
точність обчислень площі підвищується, а коливання відносно точного значення зменшується.
1.5.1. Задачі на геометричні ймовірності
1. Абонент чекає телефонного повідомлення з 2-х до 3-х годин. Знайти ймовірність того, що повідомлення поступить з 2 годин 30 хв до 2 год 40 хв.
2. У круг радіуса 
вписано правильний трикутник. Яка ймовірність того, що навмання вибрана точка круга буде внутрі трикутника ?
3. У 25 сантиметрах від центра кулі, радіус якої 15 см, знаходиться точкове джерело світла. Яка ймовірність того, що наугад взята точка на поверхні кулі буде освічена ?
4. Стержень довжиною розбитий на 3 частини. Знайти ймовірність того, що довжина кожної частини буде більшою ніж 
?
5. Диск, який швидко обертається, розділений на парне число рівних секторів, які почергово закрашені у білий або чорний кольори. По диску зробили вистріл. Знайти ймовірність того, що куля попаде в один з білих секторів. Припускається, що ймовірність попадання кулі у плоску фігуру пропорціональна площі цієї фігури.
6. На площину, яка розграфлена паралельними прямими, що знаходяться одна від одної на 6 см наудачу кинуто круг радіуса 1 см. Знайти ймовірність того, що круг не перетне ні однієї з прямих. Мається на увазі, що ймовірність попадання точки на відрізок пропорціональна довжині цього відрізка і не залежить від його розташування.
Відповіді. 1. 
. 2. 
. 3. 
. 4. 
. 5. 
. 6. 
.