Главная | Обратная связь

Теорема 33 (формула Коши).

Пусть:

f(x) и g(x) определены и непрерывны на сегменте [a, b],

f(x) и g(x) дифференцируемы в интервале (a, b),

g’(x) ¹ 0 " x Î (a, b). Тогда: $ точка c Î (a, b): . (1) (это формула Коши)

Доказательство. Прежде всего отметим, что знаменатель в левой части формулы (1) не равен нулю, то есть g(a) ¹ g(b).

В самом деле, если допустить, что g(a) = g(b), то функция g(x) будет удовлетворять всем условиям теоремы Ролля, и тогда найдется такая точка на интервале (a, b), в которой g’(x) = 0, что противоречит условию 3) нашей теоремы.

1-й способ. f(b) – f(a) = f’(c)(b – a), g(b) – g(a) = g’(c)(b – a). Разделив эти равенства друг на друга, получим формулу (1). Это доказательство не годится, так как точки c, вообще говоря, разные.

2-й способ. Введем функцию F(x) = f(x) – f(a) - (g(x) – g(a)). F(x) удовлетворяет всем условиям теоремы Ролля. В частности, F(a) = F(b) = 0. По теореме Ролля, $ точка c Î (a, b): F’(c) = 0. f’(c) - g’(c) = 0. . Теорема доказана. Формула Лагранжа является частным случаем формулы Коши в случае, когда g(x) = x. В этом случае g’(c) = 1, g(a) = a, g(b)= b.

Теорема 34 (Правило Лопиталя).

Пусть: f(x) и g(x) определены и дифференцируемы в проколотой d - окрестности точки a, Пусть f(x) = g(x) = 0, g’(x) ¹ 0 в любой точке из указанной проколотой d - окрестности точки a, $ (1) Тогда: $ = .

Доказательство. Доопределим f(x) и g(x) в точке a по непрерывности, то есть положим f(a)= g(a) = 0. Тогда f(x) и g(x) будут непрерывны в некоторой окрестности точки a.

Возьмем произвольное x ¹ a из этой окрестности и применим формулу коши для сегмента [a, x]. 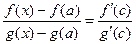, где c Î [a, x]. Отсюда получаем: . (2) Перейдем в (2) к пределу при x ® a. При этом c ® a. В силу условия 4) предел правой части равенства (2) существует, следовательно, существует предел левой части равенства, и он равен пределу правой части, то есть = . Теорема доказана

Теорема 38.

Сумма и разность двух бесконечно малых в точке a функций являются бесконечно малыми в точке а функциями.

Доказательство: Пусть f(x) и g(x)- бесконечно малые в точке x = a. Тогда " e> 0 $ > 0, > 0 " x Î {0 < | x - a | < d₁}: | f(x) | < , " x Î {0 < | x - a | < }: | g(x) | < . Положим d = min ( , ). Тогда " x Î {0 < | x - a | < d }: | f(x) ± g(x) |£ | | + | | < e. Это и означает по определению, что f(x) ± g(x) - бесконечно малые в точке x = a Теорема доказана.

Следствие. Алгебраическая сумма конечного числа бесконечно малых в точке x = a функций также является бесконечно малой в точке x = a функцией.

Теорема 39, 40, 41, 42.

Лемма 1:

Если 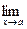f(x) = b, то f(x) можно представить в виде: f(x) = b + a(x), где a(x)- бесконечно малая в точке а.

Доказательство: Запишем функцию f(x) в виде f(x) = b + . Остаётся доказать, что a(x) = f(x) - b - бесконечно малая в функция в точке a. По определению предела функции, " e > 0 $ d > 0, " x Î {0 < | x - a | < d }: | f(x) - b | < e. То есть | a(x) | < e. Это и означает по определению, что a(x) - бесконечно малая функция в точке а. Лемма 1 доказана.

Лемма 2 (обратная лемме 1): Если f(x) = b + a(x), где b -число, a(x)-бесконечно малая функция в точке а. то 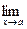f(x) = 0.

Теорема

Пусть функции f(x) и g(x) определены в некоторой проколотой окрестности точки а и пусть 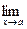f(x) = b, 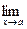f(x) = c

Тогда: 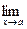[ f(x) ± g(x)] = b ± c. 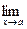f(x)g(x) = bc Если с ¹ 0, то в некоторой проколотой окрестности точки а определена функция 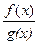(то есть g(x) ¹ 0) и = .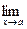

Доказательство 1.Докажем для суммы. Согласно лемме 1, f(x) и g(x) можно представить в виде: f(x) = b + a(x), g(x) = c + b(x), где a(x) и b(x)- бесконечно малые функции в точке а. f(x) + g(x) = (b + c) + [a(x) + b(x)]. Отсюда по лемме 2 следует, что 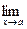[ f(x) + g(x)] = b + c. Утверждение 1 для суммы доказано.

Докажем 3.Пусть для определённости c > 0. Возьмём e = , тогда по определению предела функции $ d > 0, " x Î {0 < | x - a | < d }: | g(x) - c | < e = 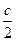. , или < . Из пдчеркнутого неравенства следует что g(x) > > 0 в проколотой d- окрестности точки а. Тем самым определена функция . По лемме 1, f(x) = b + a(x), g(x) = c + b(x), где a(x) и b(x) -бесконечно малые в точке а. Поэтому - = - = 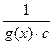(сa(x)- bb(x)). Так как < в проколотой d- окрестности точки а и сa(x)- bb(x) бесконечно малая в точке а, то - = g(х) - бесконечно малая в точке а. Итак, = + g(х), где g(х) бесконечно малая функция в точке а Следовательно, по лемме 2, = . 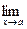Утверждение 3) доказано. Утверждение 2) доказывается таким же образом. Теорема доказана. Теорема верна также для пределов функций при х ® ¥.