 |
|
Переміщення й деформації. Взаємозв'язок між ними
Для визначення деформації пружного тіла зрівняємо положення точок тіла до й після прикладення навантаження.
Розглянемо точку 
ненавантаженого тіла і її нове положення 
після прикладення навантаження. Вектор 
називається вектором переміщення точки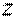 
(рис.1.4).
Рис.1.4. Вектор переміщення точки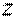
Можливі два види переміщень: переміщення всього тіла як єдиного цілого без деформування - такі переміщення вивчає теоретична механіка як переміщення абсолютно твердого тіла, і переміщення, пов'язане з деформацією тіла - такі переміщення вивчає теорія пружності.
Позначимо проекції вектора переміщення точки 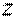на координатні осі 
через 
відповідно. Вони рівні різниці відповідних координат точок і :
і є функціями координат:
Деформування тіла викликане різницею в переміщеннях різних його точок. Нескінченно малий паралелепіпед з ребрами 
вирізаний із пружного тіла біля довільної точки 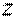, внаслідок різних переміщень його точок деформується таким чином, що змінюється довжина його ребер і спотворюються спочатку прямі кути між гранями.
На рис.1.5 показані два ребра цього паралелепіпеда: 
і 
довжина ребра 
дорівнює 
а ребра 
— 
Рис.1.5. Лінійні й кутові деформації
Після деформації точки 
приймають положення 
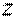При цьому точка одержить переміщення, складові якого в площині креслення рівні 
й 
Точка 
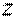віддалена від точки на нескінченно малій відстані одержить переміщення, складові якого будуть відрізнятися від складових переміщення точки 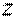на нескінченно малу величину за рахунок зміни координати 
Складові переміщення точки 
будуть відрізнятися від складових переміщення точки 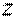на нескінченно малу величину за рахунок зміни координати 
Довжина проекції ребра 
на вісь 
після деформації:
| (1.31) |
Проекція абсолютного подовження ребра на вісь
Відносне подовження уздовж осі
| (1.32) |
називається лінійною деформацією по напрямку осі .
Аналогічно визначаються лінійні деформації по напрямках осей 
і
| (1.33) |
Розглянемо зміну кутів між ребрами паралелепіпеда (рис.1.5). Тангенс кута повороту ребра 
в площині 
Внаслідок малості деформацій 
а лінійною деформацією 
можна зневажити через її малість у порівнянні з одиницею, і тоді
Аналогічним чином можна визначити кут повороту ребра в тій же площині:
Перекручування прямого кута 
називається кутовою деформацією й визначається як сума кутів повороту ребер і :
| (1.34) |
У такий же спосіб визначаються кутові деформації у двох інших координатних площинах:
| (1.35) |
Формули (1.32)-(1.35) дають шість основних залежностей для лінійних і кутових деформацій від складових переміщення. Ці залежності називаються рівняннями Коші:
| (1.36) |
В межі, коли довжини ребер паралелепіпеда прямують до нуля, співвідношення Коші визначають лінійні й кутові деформації в околиці точки 
Позитивним лінійним деформаціям відповідають подовження, а негативним — укорочення. Кут зсуву вважається позитивним при зменшенні кута між позитивними напрямками відповідних координатних осей і негативним — у противному випадку.
Об'ємна деформація
При деформації об’єм тіла змінюється. Розглянемо нескінченно малий паралелепіпед об’єм 
З точністю до нескінченно малих вищого порядку можна вважати, що зміна об’єму обумовлена тільки зміною довжини ребер і не пов'язане зі зміною кутів зсуву.
Довжина ребра 
, що до деформації дорівнює 
(рис.1.5), після деформації, згідно (1.31), складе
або, з огляду на (1.36),
 .
| (1.37) |
Аналогічно
| (1.38) |
Добуток довжин ребер (1.37), (1.38) дає величину нового об’єму паралелепіпеда:
Розкриваючи дужки, нехтуючи величинами другого й третього порядків малості й враховуючи, що 
одержимо
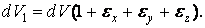
Позначимо відносну зміну об’єму
тоді
| (1.39) |
Об'ємна деформація дорівнює сумі лінійних деформацій по трьох взаємно перпендикулярних напрямках.
З огляду на (1.36), об'ємну деформацію можна виразити через складові переміщення:
| (1.40) |