 |
|
Симплексный метод выбора оптимальных решений
При решении ряда задач, связанных с принятием оптимальных решений, в том числе по обеспечению устойчивости ОЭ в ЧС, может применяться ряд методов, в частности методы линейного программирования. В простейших случаях при наличии двух-трех переменных может быть применен геометрический метод, в более сложных – симплексный метод. Задача в этих случаях заключается в отыскании наибольшего или наименьшего значений целевой функции устойчивости при наличии линейных ограничений.
Ограничения обычно задаются системой линейных уравнений
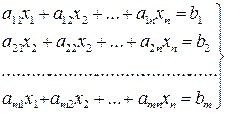 , (А)
, (А)
среди неотрицательных решений которой необходимо найти такие, которые максимизировали бы целевую функцию
L=C0+C1x1+C2x2+…+Cnxn.
Если выразить x1, x2, …, xr (r<m) через остальные переменные, то получим
 , (Б)
, (Б)
где  ,
,  , …,
, …, 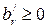 .
.
При задании ограничительных условий неравенствами, их можно преобразовать в равенства путем введения новых неотрицательных переменных, называемых балансовыми (выравнивающими). Так, например, неравенство a1x1+a2x2+…+anxn<b1 преобразуется в равенство с добавлением к его левой части некоторой величины xn+1>0, т.е. a1x1+a2x2+…+anxn+xn+1=b1. Если ограничительные условия задаются смешанным образом, т.е. неравенствами и уравнениями, их таким же образом сводят только к уравнениям. Переменные x1, x2, …, xr называются базисными, а весь набор { x1, x2, …, xr} базисом. Остальные переменные называются свободными, а система ограничений (Б) – системой, приведенной к единичному базису.
Подстановка в целевую функцию L вместо базисных переменных их выражений через свободные из системы (Б) приводит ее к виду
L=γ0+γr+1xr+1+…+γnxn.
Полагая все свободные переменные равными нулю, находят значения базисных переменных:
 ,
,  , …,
, …,  .
.
Таким образом, получается решение системы ( 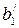 ,
, 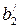 , …,
, …, 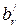 , 0, …, 0), которое называется базисным. Для полученного базисного решения значение целевой функции будет равно LБ=γ0. Решение задачи при помощи симплексного метода располагается на ряд шагов, заключающихся в том, что от данного базиса Б переходят к другому базису Б/ с таким расчетом, чтобы значение LБ уменьшалось или, по крайней мере, не увеличивалось, т. е.
, 0, …, 0), которое называется базисным. Для полученного базисного решения значение целевой функции будет равно LБ=γ0. Решение задачи при помощи симплексного метода располагается на ряд шагов, заключающихся в том, что от данного базиса Б переходят к другому базису Б/ с таким расчетом, чтобы значение LБ уменьшалось или, по крайней мере, не увеличивалось, т. е. 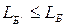 . Рассмотрим идею метода на примерах.
. Рассмотрим идею метода на примерах.
Пример.
Для герметизации административных помещений и цехов с целью защиты производственного персонала при химическом и радиоактивном заражении и обеспечения устойчивости ОЭ при радиационных и химических авариях выделено 85 тысяч рублей. На герметизацию административного помещения требуется 5 тыс. рублей, цеха 10 тыс. рублей. Найти оптимальный вариант выполнения работ, обеспечивающий укрытие наибольшего количества производственного персонала, если вместимость административного помещения 60 чел., цеха – 50 чел. На заводе 3 административных помещения и 8 цехов.
Решение.
Предположим, что решение задачи достигается при герметизации х1 административных помещений и х2 цехов. Тогда имеем следующие ограничения на переменные х1 и х2
 .
.
Целевая функция будет иметь вид L=60x1+50x2.
Преобразуем смешанную систему ограничений в систему ограничений в виде уравнений, введя новые переменные х3 и х4,
 .
.
Определим ранг матрицы  из коэффициентов при переменных системы
из коэффициентов при переменных системы
D1=1; 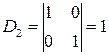 ;
;  .
.
И, следовательно, ранг матрицы равен 3. Поэтому выберем за базисные переменные х1, х2 и х3 и перейдем к единичному базису.
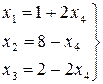 .
.
Первое допустимое решение будет при х4=0, х1=1, х2=8, х3=2. При этих значениях переменных L=60·1+50·8=460 чел.
Судя по третьему уравнению, увеличения значения целевой функции можно достигнуть путем увеличения х4 до 1. Тогда при х4=1, х1=3, х2=7, х3=0 имеем L=60·3+50·7=530 чел.
Второе допустимое решение (3, 7, 0, 1); х1=3-х3, х2=7+0,5·х3, х4=1-0,5·х3 и L=60·(3-х3)+50·(7+0,5·х3)=530-35х3.
Коэффициент при х3 в целевой функции отрицателен, а поэтому ее дальнейшие увеличение невозможно. Следовательно, оптимальное решение х1=3, х2=7 и L=530 чел.
Для осуществления итерационных операций могут применяться симплексные таблицы. Для этого систему ограничений сводят к единичному базису
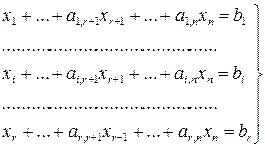 ,
,
а целевую функцию – к виду L+γr+1xr+1+…+γjxj+…+γnxn=γ0. Полученные данные сводят в таблицу
| Базисные переменные | Свободные члены | x1 | … | xi | … | xr | xr+1 | … | xj | … | xn |
| x1 | b1 | … | … | a1,r+1 | … | a1,j | … | a1,n | |||
| … | … | … | … | … | … | … | … | … | … | … | … |
| xi | bi | … | … | ai,r+1 | … | ai,j | … | ai,n | |||
| … | … | … | … | … | … | … | … | … | … | … | … |
| xr | br | … | … | ar,r+1 | … | ar,j | … | ar,n | |||
| L | γ0 | … | … | γr+1 | … | γj | … | γn |
Равенство для функции L называется приведенным (к свободным переменным) выражением, а коэффициенты γо – оценками (индексами) соответствующих свободных переменных xj.
Алгоритм итерационных операций:
1. Выбирается разрешающий столбец ap из условия чтобы была γp<0 и хотя бы один элемент aip>0.
2. Выбирается q-я разрешающая строка из условия
 для aip>0.
для aip>0.
3. Производится перерасчет элементов разрешающей q-й строки по формуле
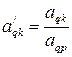 (k=0, 1, …, n).
(k=0, 1, …, n).
4. Вычисляются элементы всех остальных строк (при k≠p) по формуле
 (i=0, 1, …, q–1, q+1, …, r).
(i=0, 1, …, q–1, q+1, …, r).
При проведении итераций руководствуются основной теоремой симплексного метода, которая говорит о следующем:
Если после выполнения очередной итерации:
1. Найдется хотя бы одна отрицательная оценка и в каждом столбце с такой оценкой будет хотя бы один положительный элемент, т.е. γk<0 для некоторых k и aik>0 для тех же k и некоторого i, то можно улучшить решение, выполнив следующую итерацию.
2. Найдется хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, т.е.
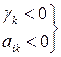
для какого-то k и всех i, то функция L не ограничена в области допустимых решений (Lmax→∞).
3. Все оценки окажутся неотрицательными, т.е. γk>0 для всех k, то достигнуто оптимальное решение.
Пример.
Для повышения противопожарной устойчивости ОЭ необходимо осуществить переподготовку инженерно-технических работников и рабочих. Определить максимально возможное количество производственного персонала, который может пройти переподготовку, если на обучение 3-х групп инженерно-технических работников можно затратить не более 18 тыс. руб., 3-х групп рабочих – 15 тыс. руб. По условиям организации, осуществляющей переподготовку, количество обучаемых в 2-х группах инженерно-технических работников и группе рабочих не должно превышать 13 чел., а в двух группах инженерно-технических работников и 3-х группах рабочих – 19 чел., при общем количестве переподготавливаемых групп ИТР – 7, рабочих – 5.
Решение.
Обозначим количество человек в группах инженерно-технических работников, прошедших переподготовку, через х1, в группах рабочих через х2. Тогда система ограничений и целевая функция могут быть представлены в виде:
 , L=7x1+5x2.
, L=7x1+5x2.
Преобразуем систему ограничений, заданную неравенствами, в систему уравнений
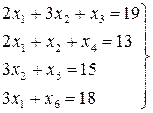 .
.
Определим ранг матрицы системы уравнений  , для чего вычислим ее миноры.
, для чего вычислим ее миноры.
D1=2,  =2·1–2·3=–4,
=2·1–2·3=–4,
 =2·1·0+3·0·0+1·2·3–1·1·0–2·0·3–3·2·0=6,
=2·1·0+3·0·0+1·2·3–1·1·0–2·0·3–3·2·0=6,
 т.е. ранг матрицы (наибольший порядок который могут иметь ее миноры, не обращающиеся в ноль) равен 4.
т.е. ранг матрицы (наибольший порядок который могут иметь ее миноры, не обращающиеся в ноль) равен 4.
Ранг расширенной матрицы 
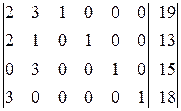 также равен 4.
также равен 4.
Поэтому четыре переменные (базисные) можно выразить через две (свободные), т.е.
 .
.
Целевую функцию представим в виде L–7x1-5x2=0. Она уже выражена через свободные переменные.
Имеем исходную табл.1:
Таблица 1
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | х6 |
 х3 х3
| |||||||
| х4 | |||||||
 х5 х5
| |||||||
| х6 | |||||||
| L | –7 | –5 |
Выясняем, имеются ли в последней (индексной) строке отрицательные оценки. Таких чисел два: –7 и –5. Выбираем любое, например –5, и просматриваем тогда столбец х2. В этом столбце есть три положительных элемента 3, 1, 3. В соответствии с методикой делим на эти числа соответствующие свободные члены получая 19/3, 13/1, 15/3. Из полученных частных наименьшее 15/3, поэтому разрешающим является элемент 3 на пересечении строки х5 и столбца х2. Выделяем эту строку и столбец рамками. Новый базис будет состоять из х3, х4, х2 и х6. Для составления следующей таблицы (табл.2) умножаем выделенную строку в табл.1 на 1/3 для того, чтобы получить на месте разрешающего элемента 1. Полученную таким образом строку пишем в табл.2 на месте прежней. К каждой из остальных строк в табл.1 прибавляем строку для х5 в табл.1, умноженную на такое число, чтобы в клетках столбца х2, появились нули, и пишем преобразованные строки в табл.2 на месте прежних. Этим завершаем первую итерацию.
Таблица 2
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | х6 |
  х3 х3
| –1 | ||||||
| х4 | –1/3 | ||||||
| х5 | 1/3 | ||||||
| х6 | |||||||
| L | –7 | 5/3 |
Повторяем все рассуждения применительно в табл.2, т.е. выполняем вторую итерацию. В последней строке единственная отрицательная оценка –7. Просматриваем столбец х1 и делим на три положительных элемента 2, 2, 3 соответствующие свободные члены, получаем 4/2, 8/2, 18/3. Из полученных частных наименьшее 4/2. Следовательно, разрешающим является элемент 2, находящийся на пересечении строки для х3 и столбца для х1. Выделяем эту строку и столбец рамками. Новый базис будет состоять из х1, х4, х2, х6.
Для составления следующей таблицы умножаем выделенную строку табл.2 на 1/2, чтобы получить на месте разрешающего элемента 1 и полученную таким образом строку пишем в следующей табл.3 на месте прежней. К каждой из остальных строк прибавляем строку для х3 в табл.2, умноженную на такое число, чтобы в клетках столбца х1 появились нули и пишем преобразованные строки на месте прежних в табл.3. Завершаем этим вторую итерацию и переходим к следующей таблице.
Таблица 3
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | х6 |
 х1 х1
| 1/2 | –1/2 | |||||
 х5 х5
| –1 | 2/3 | |||||
| х2 | 1/3 | ||||||
| х6 | –3/2 | 3/2 | |||||
| L | 7/2 | –11/6 |
То же повторим применительно к табл.3. Разрешающим элементом в табл.3 является элемент 2/3, находящийся на пересечении строки для х4 и столбца для х5. завершаем итерацию и переходим к табл.4, т.е. делим на три положительных 2/3, 1/3 и 3/2 соответствующие свободные члены 4, 5 и 12, находим наименьшее 6 и разрешающий элемент 2/3, находящийся на пересечении строки для х4 и столбца для х5, выделяем эту строку и столбец рамками, находим новый базис х1, х5, х2 и х6, умножаем выделенную строку табл. на 3/2, чтобы получить на месте разрешающего элемента 1. Полученную умножением строку записываем в табл.4 на ее прежнем месте, к каждой из остальных строк прибавляем строку для х4 в табл.3, умноженную на такое число, чтобы получить в клетках столбца х5 нули, т.е. на числа: для х1 в табл.3 «3/4», для х2 в табл.3 «–1/2», х6 в табл.3 «–9/4», L в табл. 3 «11/4». Получаемые результаты записываем в табл. 4.
Таблица 4
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | х6 |
| х3 | –1/4 | 3/4 | |||||
| х4 | –3/2 | 3/2 | |||||
| х5 | 1/2 | –1/2 | |||||
| х6 | 3/4 | –9/4 | |||||
| L | 3/4 | 11/4 |
Отсутствие в последней (индексной) строке отрицательных оценок свидетельствует о достижении оптимального решения (5, 3, 0, 0, 6, 3) и наибольшем возможном значении целевой функции L, равном 50 (Lmax=50), т.е. наибольшее количество производственного персонала, которое возможно переподготовить при условиях задачи, равно 50 чел.