 |
|
Отримання когерентних хвиль за допомогою біпризми Френеля
Одна з оптичних схем отримання когерентних хвиль здійснюється за допомогою біпризми Френеля. Для цього використовується заломлення світла від одного точкового джерела S в двох призмах з малим заломлюючим кутом  , які мають спільну основу (рис. 2.1). Така біпризма може бути також виготовлена з цільного матеріалу. Заломлюючий кут
, які мають спільну основу (рис. 2.1). Така біпризма може бути також виготовлена з цільного матеріалу. Заломлюючий кут  біпризми є малим, внаслідок чого промені відхиляються біпризмою на однаковий кут:
біпризми є малим, внаслідок чого промені відхиляються біпризмою на однаковий кут:
 ,
,
де n – показник заломлення скла, з якого виготовлена біпризма.
Джерело світла S розміщають на відстані  від основи біпризми.
від основи біпризми.
Як видно з рис. 2.1, при проходженні світла через верхню і нижню половини біпризми світлова хвиля розділяється на дві когерентні хвилі, які ніби виходять з точок  і
і  – уявних зображень джерела
– уявних зображень джерела  (при малому куті заломлення біпризми уявні джерела
(при малому куті заломлення біпризми уявні джерела  і
і  практично знаходитимуться на такій самій відстані від біпризми, що й джерело
практично знаходитимуться на такій самій відстані від біпризми, що й джерело  ).
).

При малому значенні кута  відстань
відстань 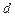 між джерелами
між джерелами  і
і  можна визначити таким чином:
можна визначити таким чином:
 . (2.3)
. (2.3)
Якщо на шляху інтерферуючих пучків поставити екран  , то в його площині буде спостерігатися чергування темних і світлих смуг.
, то в його площині буде спостерігатися чергування темних і світлих смуг.
Положення інтерференційних максимумів і мінімумів на екрані можна визначити, якщо скористатися рис. 2.2. Оскільки  і
і  – уявні зображення джерела
– уявні зображення джерела  , то їх розглядають як два когерентні точкові джерела. Результат інтерференції світлових хвиль, які доходять до деякої точки M на екрані E від джерел
, то їх розглядають як два когерентні точкові джерела. Результат інтерференції світлових хвиль, які доходять до деякої точки M на екрані E від джерел  і
і  , визначатиметься їх оптичною різницею ходу
, визначатиметься їх оптичною різницею ходу
 ,
,
де  - показник заломлення середовища;
- показник заломлення середовища;  і
і 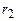 – відстані від уявних зображень джерел
– відстані від уявних зображень джерел  і
і  , відповідно.
, відповідно.

Якщо  =
=  , то в точці M буде спостерігатися інтерференційний максимум. Якщо ж
, то в точці M буде спостерігатися інтерференційний максимум. Якщо ж  =
=  , то в точці
, то в точці 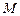 буде інтерференційний мінімум. При інших значеннях
буде інтерференційний мінімум. При інших значеннях  інтенсивність світла в точці М матиме проміжне значення.
інтенсивність світла в точці М матиме проміжне значення.
Відстань  між центральним максимумом і максимумом
між центральним максимумом і максимумом 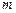 –го порядку з врахуванням того, що для малих значень кута
–го порядку з врахуванням того, що для малих значень кута 
 , дорівнює:
, дорівнює:
 , (2.4)
, (2.4)
де L - відстань щілини до екрану, а 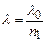 .
.
З рівняння (2.4) отримуємо:
 . (2.5)
. (2.5)
Якщо значення d з рівняння (2.3) підставити в (2.5), то довжину хвилі випромінювання можна визначити за формулою:
 . (2.6)
. (2.6)
Отримати когерентні хвилі можна також іншими методами: наприклад: методами білінзи Френеля, дзеркала Ллойда та ін.