 |
|
Водородоподобная система в квантовой механике
Состояние микрочастицы описывается в квантовой механике волновой функцией ψ. Она является функцией координат и времени. Квадрат модуля волновой функции определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:
. (8.14)
Волновая функция может быть найдена путем решения уравнения Шрёдингера:
. (8.15)
Здесь Δ – оператор Лапласа ( 
); U –потенциальная энергия частицы. Уравнение Шрёдингера является основным уравнением квантовой механики. Подобно тому, как уравнения динамики Ньютона не могут быть получены теоретически, а представляют собой обобщение большого числа опытных фактов, уравнение Шрёдингера также нельзя вывести из каких-либо известных ранее соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем обстоятельством, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.
В атоме водорода или водородоподобном ионе потенциальная энергия электрона равна:
. (8.16)
Уравнение Шрёдингера имеет в этом случае вид:
. (8.17)
Можно показать, что (8.17) имеет однозначные, конечные и непрерывные решения в следующих случаях: 1) при любых положительных значениях Е; 2) при дискретных отрицательных значениях энергии, равных:
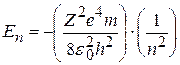, (n=1, 2, 3,…∞). (8.18)
Случай Е>0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е<0 соответствует электрону, находящемуся в пределах атома. Сравнение (8.18) и (8.10) показывает, что квантовая механика приводит к таким же значениям энергии водородного атома, какие получались и в теории Бора. Однако в квантовой механике эти значения получаются логическим путём при решении уравнения Шрёдингера. Бору же для получения такого результата пришлось вводить специальные дополнительные предположения.