Главная | Обратная связь

Понятия о комплексных и полных сопротивлениях электрической цепи

ЭЦ оказывает сопротивление переменному току Полное сопротивление цепи определяется

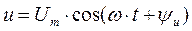
Угол сдвига фаз между гармоническим напряжением и током

Если рассматривать комплексные токи и напряжения, то можно ввести комплексное сопротивление цепи

- комплексное сопротивление

где Z полное сопротивление цепи (модуль комплексного сопротивления),

φ –сдвиг фаз между гармоническим напряжением и током (аргумент комплексного сопротивления)

R_(Э) – активное (резистивное сопротивление) эквивалентное

X_(Э) - реактивное сопротивление эквивалентное

 

Это можно пояснить математически по составляющим и через треугольник

Uа- активное напряжение совпадает по фазе с током Uр- реактивное напряжение сдвиг на π/2

 

Гармонический ток в пассивных элементах электрической цепи

1 Резистивное сопротивление

 

 

начальная фаза напряжения на резистивном сопротивлении равна фазе тока.

 

Гармонические напряжение и ток в резистивном сопротивлении совпадают по фазе.

 

2 Индуктивность.

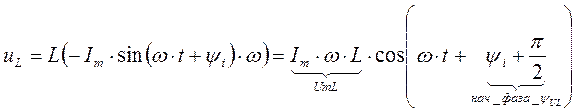
U_mL=I_mωL – амплитуда напряжения на индуктивности (пропорциональна частоте)

ωL=x_L- индуктивное сопротивление, φ_L = Ψ_UL-Ψ_i = π/2 - сдвиг фаз между индуктивным напряжением и током (индуктивное напряжение опережает ток на четверть периода (90⁰⁾).

- комплексное сопротивление индуктивного элемента, при постоянном токе (ω =0) x_L(0)=0

 

Емкость

 

 

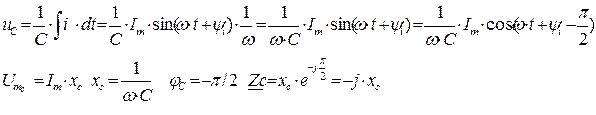
Емкостное сопротивление обратно пропорционально частоте

Емкостное напряжение отстает от тока по фазе на четверть периода (90⁰)

 

 

Анализ последовательной RLC-цепи при гармоническом воздействии

 

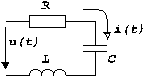
На основе второго закона Кирхгофа u = u_R+u_L+u_C или в комплексной

форме

U=U_R+U_L+U_C С учетом

 

получим

 

где - комплексное сопротивление RLC - цепи

 

Преобразовав, получаем, что ,

где - реактивное сопро­тивление, - полное сопротивление цепи, а - угол сдвига фаз RLC цепи.

 

Запишем закон Ома в комплексной форме с учетом фазовых соотношений:

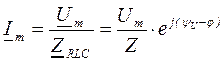. Здесь .

 

Треугольник сопротивлений в RLC – цепи.

 

- полное сопротивление RLC - цепи,

угол сдвига фаз RLC - цепи.

 

Рассмотрим зависимости полного сопротивления Z и угла сдвига фаз φ в последовательной RLC-цепи от частоты.

ω₀ – резонансная частота RLC - цепи

 

ω₀

До ω₀ напряжение отстает от тока, после ω₀ напряжение опережает ток.

Рассмотрим зависимость тока и напряжения на резисторе от частоты

 

 

;

 

 

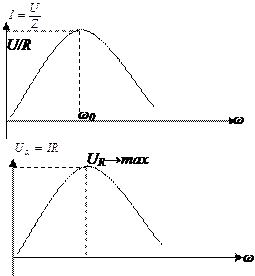
Варианты графиков U_L . U_C в RLC – цепи. Графики могут иметь максимумы.

 

 

 

 

 

 

Векторные диаграммы последовательной RLC-цепи

 

Вид диаграмм зависит от выбранной частоты по отношению к резонансной.

1) ω<ω₀., U_L < U_C

 

2) ω=ω₀ → U_L=U_C

φ=0 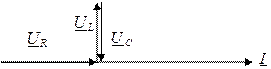3) ω>ω₀. U_L > U_C