 |
|
Графический метод решения задач линейного программирования
Очевидно, что КЗЛП относится к задачам выбора, поскольку условие  (считая ранг матрицы
(считая ранг матрицы 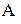 линейных ограничений равным
линейных ограничений равным  ) гарантирует в общем случае бесконечное количество допустимых решений.
) гарантирует в общем случае бесконечное количество допустимых решений.
Так как частные производные от целевой функции есть постоянные числа,
не все равные нулю:

 не может иметь экстремум во внутренних точках области допустимых решений (ОДР). Это обстоятельство серьезно увеличивает сложность решения задачи, которое в общем виде впервые было получено Л. В. Канторовичем лишь в 1939 году.
не может иметь экстремум во внутренних точках области допустимых решений (ОДР). Это обстоятельство серьезно увеличивает сложность решения задачи, которое в общем виде впервые было получено Л. В. Канторовичем лишь в 1939 году.
Ограничения, соответствующие СЗЛП, могут определять одну из следующих ситуаций:
область допустимых решений пустая – нет решения задачи;
область допустимых решений не ограничена – возможно неограниченное решение задачи (такое решение не реализуемо на практике и обычно считается невозможным);
область допустимых решений конечна и непустая. Этот вариант и рассматривается в дальнейшем.
Область допустимых решений, задаваемая линейными условиями ОЗЛП, есть выпуклый многогранник. Следовательно, задача имеет глобальный оптимум. Показано, что решение ОЗЛП лежит в так называемой угловой точке, т. е. там, где  переменных обращаются в ноль. Отсюда следует основная идея решения задачи: просмотреть допустимые угловые точки и из них выбрать ту, где W(Х) достигает максимума. На рисунке 5 представлена иллюстрация решения ОЗЛП для плоского случая
переменных обращаются в ноль. Отсюда следует основная идея решения задачи: просмотреть допустимые угловые точки и из них выбрать ту, где W(Х) достигает максимума. На рисунке 5 представлена иллюстрация решения ОЗЛП для плоского случая  Для решения задач линейного программирования разработано большое количество методов решения, для которых имеются доступные пакеты прикладных задач. Остановимся на графическом методе решения ЗЛП.
Для решения задач линейного программирования разработано большое количество методов решения, для которых имеются доступные пакеты прикладных задач. Остановимся на графическом методе решения ЗЛП.
Рассмотрим ЗЛП в канонической форме:

Как известно из линейной алгебры, если  , то система ограничений ЗЛП
, то система ограничений ЗЛП

имеет единственное решение, которое при неотрицательности всех входящих переменных будет допустимым и оптимальным.
Рассмотрим случай  . Здесь система уравнений имеет бесчисленное множество решений. Выберем
. Здесь система уравнений имеет бесчисленное множество решений. Выберем  неизвестных, таких, чтобы определитель, составленный из коэффициентов при этих неизвестных, не обращался в ноль. Пусть эта система будет иметь вид
неизвестных, таких, чтобы определитель, составленный из коэффициентов при этих неизвестных, не обращался в ноль. Пусть эта система будет иметь вид

где все коэффициенты системы однозначно определяются исходными данными.
Если переменные  принять равными нулю, то получим решение
принять равными нулю, то получим решение

которое называется базисным. Переменные  называются базисными, набор переменных
называются базисными, набор переменных  называется базисом, а переменные
называется базисом, а переменные  называются небазисными или свободными. В одной системе уравнений могут существовать несколько различных базисов. Если среди переменных базисного решения есть переменные с отрицательными значениями, то такое базисное решение являемся недопустимым.
называются небазисными или свободными. В одной системе уравнений могут существовать несколько различных базисов. Если среди переменных базисного решения есть переменные с отрицательными значениями, то такое базисное решение являемся недопустимым.
Допустимым базисным решением или опорным планом является такое базисное решение, которое одновременно и допустимо, т. е. которое дает неотрицательные значения базисных переменных:

Появление хотя бы одного 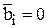 делает допустимое базисное решение вырож-
делает допустимое базисное решение вырож-
денным.
Рассмотрим сначала графический метод решения ЗЛП на примерах, а затем сформулируем общие указания к нему.
Пример 1. Решить графически ЗЛП:

Решение. Прежде всего построим область, задаваемую системой неравенств. На плоскости  проведем прямую
проведем прямую  . Затем в неравенство подставим, например, точку
. Затем в неравенство подставим, например, точку  . Очевидно, что
. Очевидно, что  поэтому неравенству будет удовлетворять та полуплоскость, в которую эта точка входит. Аналогично поступая с оставшимися неравенствами, получим пятиугольник (рис. 5).
поэтому неравенству будет удовлетворять та полуплоскость, в которую эта точка входит. Аналогично поступая с оставшимися неравенствами, получим пятиугольник (рис. 5).





Рисунок 5. Область допустимых решений ЗЛП
Далее в этой же системе координат построим вектор 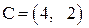 , нормальный к линиям уровня
, нормальный к линиям уровня 
Прямая, проходящая через начало координат перпендикулярно вектору, представляет собой линию уровня, соответствующую значению  . Перемещая эту прямую, параллельно самой себе в направлении вектора
. Перемещая эту прямую, параллельно самой себе в направлении вектора  до тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении линия уровня пройдет через точку
до тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении линия уровня пройдет через точку  . Этому положению линии уровня соответствует
. Этому положению линии уровня соответствует  . Для нахождения координат точки
. Для нахождения координат точки  необходимо совместно решить систему уравнений граничных прямых
необходимо совместно решить систему уравнений граничных прямых
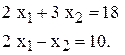
В результате получим 
Пример 3. Решить графически ЗЛП:

Решение. Построим область допустимых решений.
Она не ограничена, поэтому задача не имеет решения.
Пример 4. Решить графически ЗЛП:

Решение. Построим область допустимых решений.
Целевая функция совпадает с прямой  , поэтому задача имеет бесчисленное множество решений.
, поэтому задача имеет бесчисленное множество решений.
Задание 7
Решить графическим методом:

При выполнении задания студент подставляет вместо резервированных буквенных параметров конкретные индивидуальные характеристики: