 |
|
Теперішня вартість та ставки дисконту
Досить часто потрібно знати теперішню вартість (Present Value - РV) інвестиції. Ця вартість служить основою для порівняння прибутковості різних проектів та інвестицій за певний період. Отже, теперішня вартість — це грошова вартість майбутніх надходжень чи доходів з поправкою на ставки дисконту (капіталізації).
Дисконтна ставка — це процентна ставка, яка застосовується до майбутніх платежів, щоб врахувати ризик і непевність, пов'язану з фактором часу.
Для підрахунку теперішньої вартості слід визначити ставку дисконту, що враховувала б ризикованість певного проекту чи інвестицій. Існує просте правило:
Високий ризик означає високу ставку дисконту (капіталізації), малий ризик означає низьку дисконтну ставку.
Коли рівень ризику визначено, далі слід скоригувати майбутні доходи з урахуванням непевності часу. Загалом для оцінки дисконтних ставок використовують такі принципи:
З двох майбутніх надходжень вищу дисконтну ставку матиме те, що надійде пізніше.
Чим нижчий визначений рівень ризику, тим нижчою повинна бути ставка дисконту.
Якщо загальні процентні ставки на ринку ростуть, ростуть дисконтні ставки.
Ризик може зменшитись, якщо є перспектива ділового підйому, зниження інфляції та процентних ставок.
Припустимо, ви хочете визначити теперішню вартість $ 1000 через 3 роки; ви сподіваєтесь на щорічний рівень ризику, пов'язаний з реалізацією проектів під 10 %. Отже, якщо
тоді 
, (1.6)
де PV – теперішня вартість коштів;
FV — майбутня вартість коштів;
R — річна ставка процента;
N — кількість років.
Якщо нарахування відсотків планується більше одного разу за рік, то розрахунок проводять за формулою:
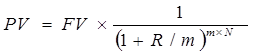, (1.7)
де т — кількість нарахувань за рік, од.
Як видно з таблиці 1, значення факторів зростає від часу і росту складного процента. Отож, якщо ці фактори підставити в знаменник останнього рівняння, теперішня вартість $ 1000 через 3 роки буде:
$ 1000 /(1+0,10)3 = $ 751
Як з’явилась ця вартість? Шляхом простого перемноження (1,10 х 1,10 х 1,10 = 1,33) та використання цього фактора для дисконтування:
$ 1000 /1,33 = $ 751
Таблиця визначення теперішньої вартості (Таблиця 2) економить багато зусиль для підрахування різних її факторів. Ця таблиця, наприклад, показує, що вартість зменшується, коли зростає проміжок часу, а також коли підвищується ставка дисконту. В таблиці наведені лише ті значення факторів, які, якщо їх перемножити на майбутню вартість, дають значення теперішньої вартості.
Очевидно, якщо ви маєте два різні проекти з однаковим періодом реалізації та витратами, але різними факторами ризику, то можна визначити їхню теперішню вартість і порівняти, який з них доцільніше вибрати. Оцінка доцільності капіталовкладень у ті чи інші проекти або інвестиції в основу бере поняття теперішньої вартості. Все зводиться до того, щоб дисконтувати майбутній доход залежно від рівня ризику та непевності майбутнього. Метод визначення теперішньої вартості дає змогу це зробити.
В останньому прикладі, де стояло завдання визначити теперішню вартість $1000 через 3 роки, досить було подивитись на кількість років та відповідний процентний фактор теперішньої вартості - (PVIF) Ргеsent Value interest Factor згідно з поданою дисконтною ставкою. Як показано, цей фактор становить 0,751. Щоб одержати теперішню вартість $1000 через З роки, маючи дисконт 10%, перемножте значення фактора на суму теперішньої вартості ($1000*(0,751=:$751). Той самий результат ви одержали шляхом довших підрахунків.
(1.8)
PVIF - фактор (множник) поточної вартості, стандартні значення якого наведені в таблиці значень фактора поточної вартості (таблиця 2).
Таблиця теперішньої вартості очевидно економить фінансистам багато часу. Зверніть увагу на те, що за пониження ставки дисконту росте значення теперішньої вартості, коли ж ставки ростуть; вартість падає. Отже, має бути зрозуміло, що поняття теперішньої вартості є важливим фактором для вибору рішення про вкладання грошей та інвестицій.
Припустімо, фірма сподівається одержати такі суми грошей за наступні чотири роки ($):
| Рік З |
Грошовий потік
Теперішня вартість всього грошового потоку є простою сумою вартості грошових потоків за кожен рік. Якщо дисконтна ставка дорівнює 10%, теперішня вартість грошових потоків за 4 роки дорівнюватиме $3642,43:
| Рік | Грошовий потік | Процентний фактор теперішньої вартості (дивись табл. 2) | Теперішня вартість |
| $1000 | 0,9091 | $909,10 | |
| $1200 | 0,8264 | $991,68 | |
| $1500 | 0,7513 | $1126,95 | |
| $900 | 0,6830 | $614,70 |
Теперішня вартість грошового потоку за 4 роки становить $3642,43.
Інвестування грошових коштів у різноманітні програми, створення грошових фондів цільового призначення, пoгaшення банківської заборгованості, тощо передбачають виплати, що здійснюватимуться через певні проміжки часу. При цьому виникає ряд послідовнихплатежів, пойменованих потоком платежів.
Ряд послідовних фіксованих платежів, що здійснюються через рівні проміжки часу, називають фінансовою рентою або ануїтетом.
Узагальнюючими показниками ануїтету є його майбутня і теперішня вартість.
Майбутня вартість ануїтету — це сума всіх членів потоків платежів з нарахованими на них процентами на кінець періоду, тобто на дату останньої виплати. Вона показує, яку величину представлятиме капітал, що вкладається через рівні проміжки часу впродовж всього терміну ануїтету разом з нарахованими процентами.
Приклад: Визначте загальну майбутню вартість платежів ануїтету на суму $100, що сплачується раз на рік вподовж чотирьох років. Візьміть складний процент 10%.
Визначити загальну майбутню вартість цих послідовних платежів не важко. Досить підсумувати фактори майбутньої вартості за кожен рік, в якому сплачується ануїтет.
За таблицею майбутньої вартості, фактор ануїтету за 4 роки за 10% складного проценту є: 1,000 + 1,100 + 1,210 + 1,33, або 4,641. Через 4 роки щорічний платіж $100 буде вартий $100*4,641, або $464,10.
Проста формула визначення майбутньої вартості ануїтету така:
, (1.9)
де: FVA — загальна майбутня вартість ануїтету на кінець визначеного періоду;
A— ануїтетні платежі;
FVIFA— ануїтетний фактор, або процентний фактор майбутньої вартостіануїтету (Таблиця 3).
Таблиці майбутньої вартості ануїтету полегшують підрахунки, в них вже підсумовані проміжні процентні фактори майбутньої вартості ануїтету і дається один фактор. Таблиця — це стандартна таблиця майбутньої вартості ануїтету. Використовуючи дані з попереднього прикладу, визначимо фактор 4-річного ануїтету. Він становить 4,641.
Коли фінансові менеджери стоять перед тим, що в майбутньому постійно, регулярно надходитимуть гроші і їм треба визначити теперішню вартість тих надходжень, вони можуть зробити дві речі:
1. Вирахувати теперішню вартість надходжень за кожен рік, використовуючи відповідні фактори. Але це довга й клопітна справа.
2. Вирахувати теперішню вартість ануїтету, використовуючи фактори теперішньої вартості ануїтету. Це коротший і найпростіший шлях.
Один приклад допоможе вам зрозуміти, що легше. Припустімо, ви очікуєте грошовий доход на суму $100 протягом 3 років щорічно і хочете визначити теперішню вартість цих доходів залежно від рівня ризику або ж ставку дисконту —- 10%. Якщо ви використаєте довгий підрахунок, то вам треба знайти фактори в таблиці теперішньої вартості, визначити теперішню вартість суми $100 за кожен з трьох років і підсумувати значення:
| Рік | Грошовий потік | Фактор Р (10%) | Теперішня вартість |
| $100 | 0,909 | $90,90 | |
| $100 | 0,826 | $82,60 | |
| $100 | 0,751 | $75,10 | |
| Всього | 2,486 | $248,60 |
Згадайте, як ми розглядали майбутню вартість ануїтетів і зазначали, що фактори вартості ануїтетів — це сума факторів майбутньої вартості. Той самий принцип застосовується, коливизначається теперішня вартість ануїтетів для серії однакових надходжень майбутніх грошових потоків. Все, що треба зробити, це скласти фактори теперішньої вартості за певний період помножити одержаний загальний ануїтетний фактор на грошовий потік за будь-який рік.
ТЕМА 7. ОЦІНКА РЕЗУЛЬТАТІВ РЕАЛІЗАЦІЇ ПРОЕКТНИХ РІШЕНЬ
1. Основні показники оцінки проекту
2. Особливості оцінки ІТ проектів