 |
|
Интегральный признак.
Теорема (интегральный признак сходимости Коши-Маклорена).
Пусть дан ряд
,
члены которого положительны и не возрастают.
Пусть 
-- функция, которая определена для всех действительных 
, непрерывна, не возрастает и такая, что
,
тогда для сходимости ряда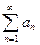 
необходимо и достаточно, чтобы сходился (существовал) интеграл
.
Достоинство интегрального признака состоит в его высокой чувствительности. Он во многих случаях позволяет устанавливать сходимость или расходимость рядов, которые удовлетворяют необходимому условию сходимости, но для которых общий член ряда убывает медленно (признак Даламбера не работает).
Сформулируем важное следствие интегрального признака: если положительный ряд можно исследовать на сходимость по интегральному признаку, то его остаток оценивается по формуле:
.
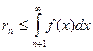Эта оценка используется для приближенного вычисления суммы сходящихся рядов.
Задача №5.Исследовать на сходимость ряд 
.
Решение. Воспользуемся интегральным признаком. Введем функцию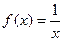 
, такую, что 
.
Рассмотрим несобственный интеграл
,
и исследуем его на сходимость:
,
интеграл расходится, поэтому должен расходиться и ряд.
Ответ: ряд расходится.
Задача №6. Исследовать на сходимость ряд 
.
Решение. 
, 
,
,
несобственный интеграл сходится (равен конечному числу), следовательно, по интегральному признаку ряд сходится.
Ответ: ряд сходится.
Ряд называется гармоническим, а ряд вида 
при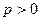 
называется рядом Дирихле или обобщенным гармоническим рядом. Как было показано в примерах , эту группу рядов можно исследовать на сходимость с помощью интегрального признака:
Утверждение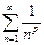 
--сходится при 
и расходится при 
.
Задача №7.Исследовать на сходимость ряд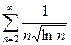 
.
Решение. 
, 
,
вычислим несобственный интеграл, используя метод замены переменной:
Согласно интегральному признаку из расходимости интеграла следует расходимость ряда.
Ответ: ряд расходится.