 |
|
Абсолютная и условная сходимость.
Все представленные выше достаточные признаки сходимости применимы только к рядам с положительными членами, какие мы и рассматривали до сих пор.
Перейдем к рассмотрению знакопеременных рядов.
Знакопеременным называется ряд, который содержит как положительные, так и отрицательные слагаемые. Опишем методы исследования таких рядов.
Важную информацию о поведении такого ряда можно получить, рассматривая ряд, членами которого являются абсолютные величины членов исходного ряда.
Определение. Рассмотрим ряд
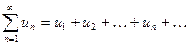 ,
,
где 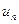 -- числа произвольного знака. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
-- числа произвольного знака. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
Теорема.Если ряд сходится абсолютно, то он сходится.
Другими словами, из сходимости ряда, составленного из модулей знакопеременного ряда, вытекает сходимость самого знакопеременного ряда.
Ряд, составленный из модулей членов знакопеременного ряда, является, очевидно, положительным и, следовательно, к нему применимы все рассмотренные выше признаки сходимости положительных рядов.
Задача №1.Исследовать на сходимость ряд 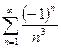 .
.
Решение. Исследуем ряд на абсолютную сходимость. Для этого запишем ряд
 .
.
Получили положительный ряд, который сходится, так как является обобщенным гармоническим при  . Делаем вывод, что исходный знакопеременный ряд сходится абсолютно.
. Делаем вывод, что исходный знакопеременный ряд сходится абсолютно.
Ответ: ряд сходится абсолютно.
Задача №2.Исследовать на сходимость ряд 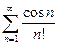 .
.
Решение. Данный ряд является знакопеременным, поскольку знак выражения  меняется. Рассмотрим ряд, состоящий из модулей исходного ряда:
меняется. Рассмотрим ряд, состоящий из модулей исходного ряда:
 .
.
Получившийся положительный ряд можно исследовать на сходимость с помощью первого признака сравнения. Для любого натурального 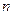 справедливо неравенство:
справедливо неравенство:
 .
.
Ряд 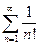 сходится, что можно показать по признаку Даламбера,
сходится, что можно показать по признаку Даламбера,
следовательно, по первому признаку сравнения положительный ряд 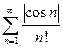 сходится, а исходный знакопеременный ряд
сходится, а исходный знакопеременный ряд 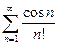 сходится абсолютно.
сходится абсолютно.
Ответ: ряд сходится абсолютно.
Заметим, что положительные ряды сходятся (имеют конечную сумму) за счет «достаточно быстрого» стремления к нулю общего члена ряда, для знакопеременных рядов существует еще одна причина сходимости: сумма стабилизируется за счет вычитания слагаемых. Поэтому для знакопеременных рядов может возникнуть ситуация, когда ряд, составленный из модулей, расходится, а сам знакопеременный ряд сходится. В этом случае говорят об условной сходимости.
Определение. Знакопеременный ряд называется условно сходящимся, если он сходится, но не сходится абсолютно.
Примеры условно сходящихся рядов мы приведем в следующем разделе.