 |
|
Приближенное вычисление суммы числового ряда.
Поскольку точное значение суммы ряда удается вычислить далеко не всегда (такие задачи были нами рассмотрены), возникает проблема приближенного вычисления суммы ряда с заданной точностью.
Напомним, что 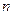 -ый остаток ряда
-ый остаток ряда  получается из исходного ряда
получается из исходного ряда 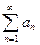 отбрасыванием первых
отбрасыванием первых 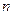 слагаемых:
слагаемых:
 .
.
Тогда, поскольку для сходящегося ряда 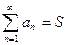 ,
,
остаток сходящегося ряда равен разности между суммой ряда и 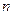 -ой частичной суммой:
-ой частичной суммой:
 ,
,
и для достаточно больших 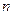 имеем приближенное равенство
имеем приближенное равенство
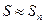 .
.
Из определения остатка ряда следует, что абсолютная погрешность при замене точного неизвестного значения суммы  его частичной суммой
его частичной суммой 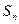 равна модулю остатка ряда:
равна модулю остатка ряда:
 .
.
Таким образом, если требуется вычислить сумму ряда с заданной точностью  , то нужно оставить сумму такого числа
, то нужно оставить сумму такого числа 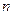 слагаемых, чтобы для отброшенного остатка ряда выполнялось неравенство:
слагаемых, чтобы для отброшенного остатка ряда выполнялось неравенство:
 .
.
Метод приближенного вычисления суммы выбирается в зависимости от вида ряда:
если ряд положительный и может быть исследован на сходимость по интегральному признаку (удовлетворяет условиям соответствующей теоремы), то для оценки суммы используем формулу
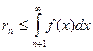 ;
;
если это ряд Лейбница, то применяем оценку:
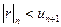 .
.
В других задачах можно использовать формулу суммы бесконечно убывающей геометрической прогрессии.
Задача №1.Сколько нужно взять слагаемых ряда 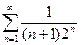 , чтобы получить его сумму с точностью 0,01.
, чтобы получить его сумму с точностью 0,01.
Решение. Прежде всего, отметим, что данный ряд сходится. Рассмотрим 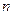 -ый остаток ряда, который и является погрешностью вычислений суммы ряда:
-ый остаток ряда, который и является погрешностью вычислений суммы ряда:
 .
.
Оценим этот ряд с помощью бесконечно убывающей геометрической прогрессии. Для этого заменим в каждом слагаемом множитель 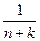 на
на  , при этом каждое слагаемое увеличится:
, при этом каждое слагаемое увеличится:

После вынесения общего множителя за скобки, в скобках остается ряд, составленный из членов бесконечно убывающей геометрической прогрессии, сумму которого мы и вычислили по формуле
 .
.
Заданная точность будет достигнута, если 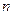 будет удовлетворять условию
будет удовлетворять условию
 .
.
Решим неравенство, учитывая, что 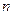 - целое.
- целое.
При 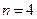 имеем
имеем
 .
.
При 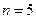 имеем
имеем
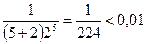 .
.
В силу монотонности функции 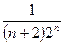 , неравенство
, неравенство  будет выполняться для всех
будет выполняться для всех  .
.
Следовательно, если вместо точного значения суммы мы возьмем первые пять (или более) слагаемых, то погрешность вычислений не превысит 0,01.
Ответ:  .
.
Задача №2.Оценить ошибку, получаемую при замене суммы ряда 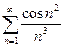 суммой первых 100 слагаемых.
суммой первых 100 слагаемых.
Решение. Заметим, что данный ряд является сходящимся и знакопеременным. Оценивать будем ряд 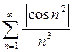 , состоящий из модулей исходного ряда, что сразу увеличивает погрешность вычислений. Кроме того, нам придется перейти (используя признак сравнения) к мажорирующему, более простому сходящемуся ряду:
, состоящий из модулей исходного ряда, что сразу увеличивает погрешность вычислений. Кроме того, нам придется перейти (используя признак сравнения) к мажорирующему, более простому сходящемуся ряду:
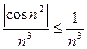 .
.
Рассмотрим ряд 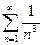 . Поскольку этот ряд удовлетворяет условиям теоремы – интегрального признака сходимости, то для оценки погрешности вычисления суммы используем соответствующую формулу:
. Поскольку этот ряд удовлетворяет условиям теоремы – интегрального признака сходимости, то для оценки погрешности вычисления суммы используем соответствующую формулу:
 .
.
Вычислим несобственный интеграл:
 ,
,
погрешность вычислений можно оценить по формуле
 ,
,
по условию  , тогда
, тогда  .
.
Ответ:  .
.
Задача №3. Оценить ошибку, получаемую при замене суммы ряда 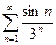 суммой первых 10 слагаемых.
суммой первых 10 слагаемых.
Решение. Подчеркнем еще раз, что задача о приближенном вычислении суммы имеет смысл только для сходящегося ряда, поэтому, прежде всего отметим, что данный ряд сходится. Поскольку исследуемый ряд является знакопеременным со сложным правилом изменения знака, то оценивать придется, как и в предыдущем примере, ряд из модулей данного ряда:
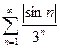 .
.
Используя тот факт, что 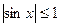 при любом значении аргумента, имеем:
при любом значении аргумента, имеем:
 .
.
Оценим остаток ряда:
 .
.
Мы получили ряд, составленный из членов бесконечно убывающей геометрической прогрессии, в которой
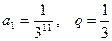 ,
,
его сумма равна:
 ,
,
 .
.
Ответ:  .
.
Задача №4.Вычислить сумму ряда  с точностью 0,01.
с точностью 0,01.
Решение. Данный ряд является рядом Лейбница. Для оценки погрешности верна формула:
 ,
,
другими словами, погрешность вычислений меньше модуля первого отброшенного слагаемого. Подберем номер 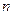 так, чтобы
так, чтобы
 .
.
При 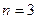 имеем
имеем
 .
.
При 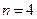 имеем
имеем
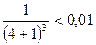 .
.
Погрешность 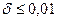 , если в качестве значения суммы возьмем сумму первых четырех слагаемых:
, если в качестве значения суммы возьмем сумму первых четырех слагаемых:
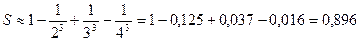 .
.
Ответ:  .
.