 |
|
Ряд Тейлора. Использование степенных рядов в приближенных вычислениях.
Рассмотрим задачу разложения некоторой функции в степенной ряд.
Пусть задана функция  , имеющая на некотором интервале производные всех порядков, тогда она разлагается на этом интервале в ряд вида
, имеющая на некотором интервале производные всех порядков, тогда она разлагается на этом интервале в ряд вида
 ,
,
который называется рядом Тейлора. Здесь 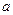 -- заданное число.
-- заданное число.
Формально ряд Тейлора можно написать для всякой функции, которая в окрестности точки 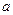 имеет производные любого порядка. Однако этот ряд будет сходиться к породившей ее функции только при тех значениях
имеет производные любого порядка. Однако этот ряд будет сходиться к породившей ее функции только при тех значениях 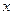 , при которых остаток ряда стремиться к нулю:
, при которых остаток ряда стремиться к нулю:
 .
.
Остаток ряда Тейлора записывается в форме Лагранжа следующим образом:
 ,
,
где  заключено между
заключено между 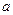 и
и 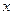 .
.
Если  , то получаем частный случай ряда Тейлора, который иногда называют рядом Маклорена:
, то получаем частный случай ряда Тейлора, который иногда называют рядом Маклорена:
 .
.
Рассмотрим ряды Тейлора для некоторых элементарных функций.

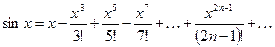

 --
--
данный ряд называется биномиальным, поскольку при натуральном  из него получается формула степени бинома.
из него получается формула степени бинома.
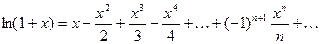
Подчеркнем, что степенные ряды для функций 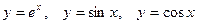 сходятся к соответствующим функциям при
сходятся к соответствующим функциям при  , а степенные ряды для функций
, а степенные ряды для функций  и
и 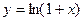 сходятся лишь при
сходятся лишь при 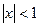 . (Для
. (Для 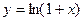 при
при  ).
).
Задача №1.Написать разложение в степенной ряд функции 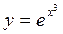 .
.
Решение. В качестве исходной формулы возьмем разложение в ряд Маклорена
функции 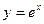 :
:
 .
.
Заменим 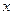 на
на 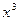 :
:

Ответ: 
Задача №2.Написать разложение в степенной ряд функции  .
.
Решение. Запишем биномиальный ряд
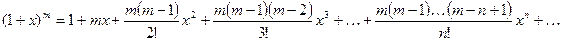
и сделаем в нем замену 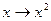 :
:

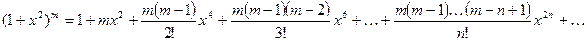 .
.
По условию  , подставим это значение в предыдущую формулу:
, подставим это значение в предыдущую формулу:
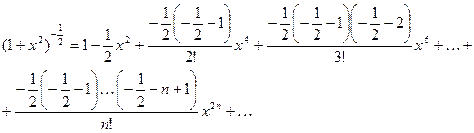
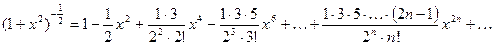
Ответ: 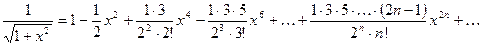 .
.
Степенные ряды широко используются в приближенных вычислениях. Рассмотрим применение рядов Тейлора для приближенного вычисления значений функций, значений определенных интегралов и приближенного решения дифференциальных уравнений.
Задача №3.Вычислить  приближенно с точностью 0,0001.
приближенно с точностью 0,0001.
Решение. Для любого 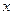 имеет место формула:
имеет место формула:
 .
.
При 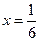 получим
получим
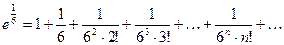 .
.
Оценим погрешность вычислений с помощью остаточного члена в форме Лагранжа:
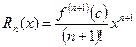 .
.
Так как
 , то
, то
 ,
,
где  лежит между
лежит между  и
и 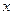 .
.
При 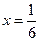 имеем
имеем
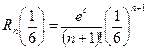 ,
,
где 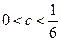 .
.
Учитывая, что 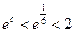 , получим
, получим
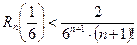 .
.
При 
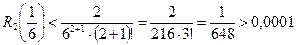 .
.
При 
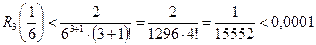 .
.
Таким образом, для достижения требуемой точности достаточно взять  (или более):
(или более):
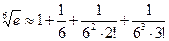 .
.
Каждое слагаемое вычислим с одним дополнительным знаком после запятой, чтобы к нашей ошибке не добавлялись ошибки от округления:
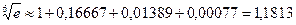 .
.
Ответ: с точностью 0,0001  .
.
Задача №4.Вычислить 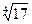 приближенно с точностью 0,0001.
приближенно с точностью 0,0001.
Решение. Для вычисления 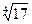 будем использовать биномиальный ряд, который сходится только при
будем использовать биномиальный ряд, который сходится только при 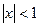 , поэтому сначала преобразуем данный корень:
, поэтому сначала преобразуем данный корень:
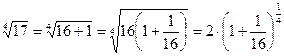 .
.
В биномиальном ряде положим  :
:

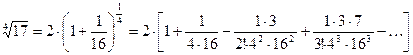 .
.
Данный знакочередующийся числовой ряд является рядом Лейбница. Чтобы определить, сколько взять первых членов ряда для вычисления 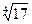 с точностью 0,0001, вычислим последовательно несколько первых членов ряда:
с точностью 0,0001, вычислим последовательно несколько первых членов ряда:
 .
.
Согласно свойству ряда Лейбница, если оставить первые три слагаемые, то ошибка искомого приближенного значения корня будет меньше 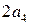 :
:
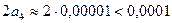 ,
,
следовательно,
 .
.
Ответ: с точностью 0,0001 
Пусть необходимо посчитать определенный интеграл
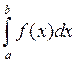
от некоторой функции  , первообразная которой не вычисляется в элементарных функциях. Следовательно, формулу Ньютона-Лейбница применить не удается. Если
, первообразная которой не вычисляется в элементарных функциях. Следовательно, формулу Ньютона-Лейбница применить не удается. Если  разложима в степенной ряд на отрезке
разложима в степенной ряд на отрезке  , принадлежащем области сходимости ряда, то интеграл может быть вычислен приближенно. Иногда приближенного вычисления бывает достаточно и при наличии первообразной функции. Для решения такой задачи используются ряды Тейлора. Рассмотрим примеры.
, принадлежащем области сходимости ряда, то интеграл может быть вычислен приближенно. Иногда приближенного вычисления бывает достаточно и при наличии первообразной функции. Для решения такой задачи используются ряды Тейлора. Рассмотрим примеры.
Задача №5.Вычислить определенный интеграл 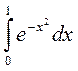 с точностью 0,01.
с точностью 0,01.
Решение. Заметим, что этот широко используемый интеграл не выражается в элементарных функциях.
В ряде Маклорена для функции 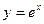 сделаем замену
сделаем замену  :
:
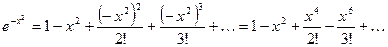 .
.
Теперь воспользуемся теоремой о том, что степенной ряд можно почленно интегрировать по любому отрезку, принадлежащему интервалу сходимости. Данный ряд сходится на всей числовой прямой, следовательно, его можно интегрировать по любому отрезку, в том числе по отрезку  :
:
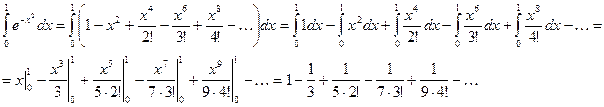
Мы получили числовой ряд, который равен значению определенного интеграла.
Оценим погрешность вычислений. Данный ряд – это ряд Лейбница, следовательно, погрешность вычислений не превосходит по модулю первого отброшенного члена ряда. Поэтому, вычисляя по порядку члены ряда, первым отбросим тот, который окажется по модулю меньше заданной точности:
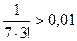 ,
,
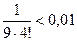 .
.
Тогда 
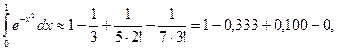 024=0,743.
024=0,743.
Ответ:  0,743.
0,743.
Задача №6.Вычислить определенный интеграл  с точностью 0,001.
с точностью 0,001.
Решение. Вычислить этот интеграл по формуле Ньютона-Лейбница нельзя, поскольку первообразная функции  не выражается в элементарных функциях. Используем для решения задачи степенной ряд. Запишем разложение в ряд Маклорена функции
не выражается в элементарных функциях. Используем для решения задачи степенной ряд. Запишем разложение в ряд Маклорена функции 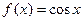 :
:
 .
.
Сделаем в этой формуле замену  :
:

Данный ряд можно почленно проинтегрировать по отрезку  :
:

Таким образом, вычисляемый определенный интеграл равен сумме знакочередующегося числового ряда, который удовлетворяет условиям признака Лейбница, следовательно, погрешность вычислений не превосходит модуля первого из отброшенных членов ряда.
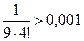 ,
,  .
.
Поэтому для достижения заданной точности необходимо оставить первые 3 слагаемые.
 .
.
Ответ:  .
.
Задача №7.. Вычислить определенный интеграл 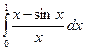 с точностью 0,001.
с точностью 0,001.
Решение. Распишем ряд Маклорена для функции 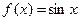 .
.
 .
.
Тогда
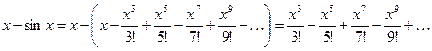 .
.
Поделим левую и правую часть формулы на 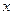 :
:
 .
.
Полученный степенной ряд можно почленно проинтегрировать по отрезку  .
.
 .
.
Получившийся числовой ряд сходится по признаку Лейбница, поэтому отбрасываем первым слагаемое, которое меньше объявленной точности:
 ,
, 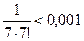 .
.
 .
.
Ответ: 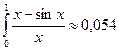 .
.
Рассмотрим еще одно приложение степенных рядов, к приближенному решению дифференциальных уравнений. Решение дифференциального уравнения не всегда можно выразить в элементарных функциях. Интегралы многих дифференциальных уравнений могут быть представлены в виде степенного ряда, сходящегося в некотором интервале значений независимой переменной. В таком случае ряд, являющийся решением дифференциального уравнения можно найти с помощью рядов Тейлора.
Пусть необходимо найти частное решение дифференциального уравнения с заданными начальными условиями, т.е. решить задачу Коши.
Проиллюстрируем решение на примере.
Задача №8.Найти первые пять членов разложения в степенной ряд решения дифференциального уравнения 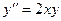 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям
 .
.
Решение. Будем искать частное решение дифференциального уравнения в виде ряда
 .
.
Мы выбрали разложение в ряд Маклорена, поскольку в условии задачи нам даны значения искомой функции и ее первой производной в точке  . Для того, чтобы найти приближенное значение функции
. Для того, чтобы найти приближенное значение функции  , нам необходимо знать значения ее второй, третьей и четвертой производных в точке
, нам необходимо знать значения ее второй, третьей и четвертой производных в точке  . Значения самой функции и первой производной в нуле даны по условию.
. Значения самой функции и первой производной в нуле даны по условию.
Значение второй производной при  найдем из дифференциального уравнения, подставив начальные условия:
найдем из дифференциального уравнения, подставив начальные условия:
 .
.
Для нахождения третьей производной продифференцируем данное дифференциальное уравнение:
 .
.
При этом необходимо учесть, что 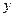 -- это функция, а
-- это функция, а 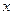 -- независимая переменная:
-- независимая переменная:
 .
.
Теперь можно вычислить значение третьей производной в точке  :
:
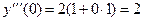 .
.
Аналогично вычислим значение четвертой производной:
 , или
, или
 .
.
Подставив в найденное равенство значения
 получим:
получим:
 .
.
Осталось подставить вычисленные в заданной точке значения производных в ряд Маклорена:
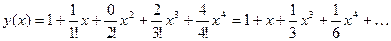 .
.
Ответ: 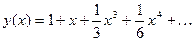 .
.
Задача №9.Найти первые четыре члена разложения в степенной ряд решения дифференциального уравнения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям
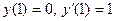 .
.
Решение. Начальные условия заданы в точке  , поэтому решение будем искать в виде ряда Тейлора:
, поэтому решение будем искать в виде ряда Тейлора:
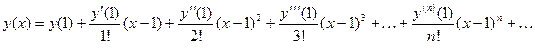 .
.
Значения самой функции и ее первой производной даны в условии задачи. Вторую производную в точке  найдем из дифференциального уравнения:
найдем из дифференциального уравнения:
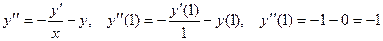 .
.
Вычислим третью производную, продифференцировав дифференциальное уравнение:
 или
или
 .
.
Тогда значение третьей производной равно
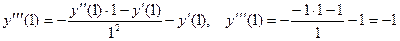 .
.
Осталось записать искомый ряд:
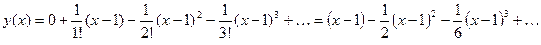
Ответ: 
Ряды Фурье.
Мы рассмотрели ряды Тейлора, в которых функция разлагалась в ряд по системе многочленов
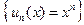 ,
,  .
.
Существуют другие способы разложения функции в ряд. Например, можно разложить функцию в ряд по системе тригонометрических функций. Такое представление широко применяется для описания различных периодических процессов или функций, заданных на отрезке, которые можно доопределить на всю числовую прямую как периодические.
Рассмотрим функцию  , периодическую с периодом
, периодическую с периодом 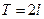 .
.
Определение. Ряд вида
 , где
, где
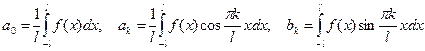
называется рядом Фурье для заданной функции  .
.
Для того, чтобы функцию можно было разложить в ряд Фурье она должна быть кусочно непрерывной, кусочно монотонной и ограниченной (т.н. условия Дирихле), то есть требуются гораздо более простые условия, чем для разложения в ряд Тейлора.
Если функция  имеет период
имеет период 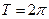 , то получаем в качестве частного случая следующее разложение в ряд Фурье:
, то получаем в качестве частного случая следующее разложение в ряд Фурье:
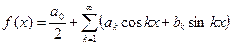 ,
, 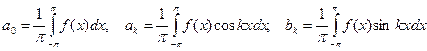 .
.
Рассмотрим примеры.
Задача №1.Разложить в ряд Фурье функцию 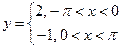 .
.
Решение. Данную функцию продолжим на всю числовую прямую как периодическую с периодом 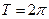 , тогда ряд Фурье для нее будет иметь вид:
, тогда ряд Фурье для нее будет иметь вид:
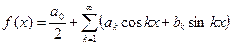 .
.
Необходимо найти коэффициенты разложения  . Функция задана на интервале
. Функция задана на интервале 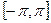 разными формулами, поэтому при вычислении разобьем интеграл на два:
разными формулами, поэтому при вычислении разобьем интеграл на два:
 .
.
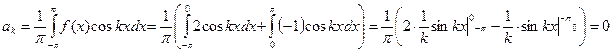 .
.
Напомним, что  при
при 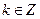 .
.

 При вычислениях использовали, что
При вычислениях использовали, что 
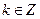 .
.
Таким образом, ряд Фурье для заданной функции имеет вид:
 .
.
Ответ:  .
.
Задача №2. Разложить в ряд Фурье функцию 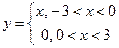 .
.
Решение. Период функции равен  , следовательно, используем ряд вида
, следовательно, используем ряд вида
 .
.
Вычислим коэффициенты ряда:
 .
.
Функция, как и в предыдущем примере, задана разными формулами, поэтому отрезок интегрирования разбиваем на части.
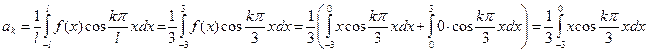 Интеграл вычисляется по частям:
Интеграл вычисляется по частям:  , тогда
, тогда

Осталось подставить найденные коэффициенты.
Ответ: 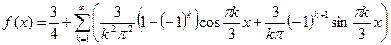 .
.
Вычисление коэффициентов ряда Фурье значительно упрощается, если известно, что данная функция является четной или нечетной на отрезке  . В случае четности функции, в разложении остаются лишь четные слагаемые, содержащие
. В случае четности функции, в разложении остаются лишь четные слагаемые, содержащие  , а все коэффициенты
, а все коэффициенты  при
при  равны нулю.
равны нулю.
Если  -- четная, то ряд Фурье имеет вид:
-- четная, то ряд Фурье имеет вид:
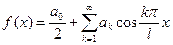 , где
, где
 .
.
Если  -- нечетная, то наоборот, ряд состоит из нечетных функций
-- нечетная, то наоборот, ряд состоит из нечетных функций  , а все коэффициенты
, а все коэффициенты 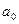 и
и  равны нулю:
равны нулю:
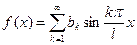 , где
, где
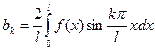 .
.
Рассмотрим теперь задачу о разложении в ряд Фурье непериодической функции, заданной на отрезке 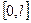 . В этом случае можно продлить функцию на всю числовую прямую как четную или как нечетную и воспользоваться формулами разложения в ряд четной или нечетной функции. Тогда периодом функции назначается отрезок
. В этом случае можно продлить функцию на всю числовую прямую как четную или как нечетную и воспользоваться формулами разложения в ряд четной или нечетной функции. Тогда периодом функции назначается отрезок  . И разложение называется соответственно разложением в ряд Фурье по синусам или косинусам.
. И разложение называется соответственно разложением в ряд Фурье по синусам или косинусам.
Задача №3.Разложить в ряд Фурье по косинусам функцию 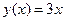 на отрезке
на отрезке  .
.
Решение. Подчеркнем, что при такой подстановке задачи функция считается заданной на полупериоде, т.е.  . Ряд по косинусам имеет вид:
. Ряд по косинусам имеет вид:
 .
.
Вычислим коэффициенты:
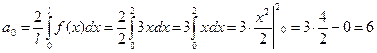 ;
;

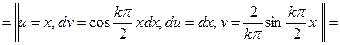

Осталось записать ответ.
Ответ:  .
.
Аналогично решается задача о разложении функции в ряд Фурье по синусам, при этом 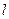 -- это по-прежнему длина отрезка, на котором задана функция:
-- это по-прежнему длина отрезка, на котором задана функция:
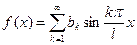 , где
, где
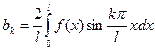 .
.