 |
|
Знакочередующиеся ряды. Признак Лейбница.
Введем понятие знакочередующегося ряда:
Определение. Ряд, в котором соседние члены имеют противоположный знак, называется знакочередующимся. Знакочередующийся ряд может быть записан в одном из двух видов:
1) 
, где 
для всех 
или
2) 
, где для всех
Знакочередующиеся ряды являются частным случаем знакопеременных.
Для знакочередующихся рядов имеет место достаточный признак сходимости, принадлежащий Лейбницу.
Теорема (признак Лейбница сходимости знакочередующихся рядов).
Если для знакочередующегося ряда
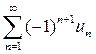или 
( для всех )
выполняются два условия:
1. Модули членов ряда монотонно (нестрого) убывают:
2. Модуль общего члена ряда стремится к нулю, т.е.
,
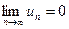то данный ряд сходится.
Подчеркнем, что все условия признака Лейбница являются существенными и подлежат проверке при применении признака Лейбница.
Договоримся далее по тексту ряд, удовлетворяющий условиям признака Лейбница называть рядом Лейбница.
Можно показать, что для сходящегося ряда Лейбница верна оценка суммы этого ряда:
.
Отсюда вытекает оценка для суммы остатка ряда Лейбница (который сам является, очевидно, рядом Лейбница):
.
Последнее неравенство часто используется для приближенного вычисления суммы сходящегося ряда.
Задача №3. Исследовать на сходимость ряд 
.
Решение. Покажем, что данный ряд является рядом Лейбница.
Действительно, присутствует чередование знаков, т.к.
а 
1) Имеем монотонное убывание модулей членов ряда, поскольку для всех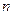 
верно неравенство:
.
2) Второе условие также выполняется: 
.
По признаку Лейбница делаем вывод о том, что ряд сходится.
Заметим, что ряд, составленный из модулей членов исходного ряда расходится (это гармонический ряд), поэтому исходный ряд сходится условно.
Ответ: ряд сходится.
Задача №4.Исследовать на сходимость ряд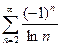 
.
Решение. Проверим выполнение условий признака Лейбница.
Чередование знака обеспечивает множитель 
, знаменатель при этом остается больше нуля:
, для всех натуральных 
.
1) Из монотонного возрастания функции 
следует, что для всех выполняется неравенство:
, отсюда
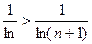, т. е. 
.
2) Справедливо и второе условие: 
.
Ряд сходится по признаку Лейбница.
Ответ: ряд сходится (условно).
Задача №5.Исследовать на сходимость ряд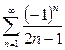 
. Установить тип сходимости (абсолютная или условная).
Решение. а). Исследуем ряд на абсолютную сходимость. Для этого рассмотрим ряд
.
Полученный положительный ряд сравним с гармоническим рядом 
:
, 
,
тогда 
Тогда по второму признаку сравнения ряд 
в смысле сходимости ведет себя также как расходящийся гармонический ряд 
. Ряд расходится, следовательно, исходный ряд 
не является абсолютно сходящимся.
б). Исследуем ряд на условную сходимость. Воспользуемся признаком Лейбница.
Ряд -- знакочередующийся, т.к. 
для всех натуральных 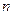, а
.
1) 
, тогда
,
что и означает монотонное убывание модулей членов ряда.
2) Верно, что 
.
Ряд сходится по признаку Лейбница.
Ответ: ряд сходится условно.
В заключение параграфа приведем две теоремы, указывающие на различие между абсолютно и условно сходящимися рядами.
ТЕОРЕМА 1
1)В абсолютно сходящемся ряде сумма всех положительных членов ряда и сумма всех отрицательных членов ряда – это конечные числа.
2) В условно сходящемся ряде сумма всех положительных членов ряда равна плюс бесконечности, а сумма всех отрицательных членов ряда равна минус бесконечности.
ТЕОРЕМА 2
1) Порядок суммирования членов абсолютно сходящегося ряда можно изменить произвольным образом. При этом ряд остается сходящимся, и его сумма не меняется.
2) Порядок суммирования членов условно сходящегося ряда можно изменить таким образом, что получившийся новый ряд будет сходиться к любому наперед заданному числу или расходится к плюс бесконечности или к минус бесконечности.
Таким образом, абсолютно сходящийся ряд близок по свойствам к конечной сумме.
Сходимость условно сходящегося ряда «зыбкая» и сильно зависит от порядка суммирования.