 |
|
Признаки сравнения положительных рядов.
К числу достаточных признаков сходимости относятся признаки, позволяющие выяснить вопрос о сходимости некоторого ряда с помощью другого ряда, поведение которого в смысле сходимости нам известно. Такие признаки называются признаками сравнения.
Теорема 1.(первый признак сравнения рядов с положительными членами).
Если ряд с положительными членами
сравнить с другим рядом с положительными членами
,
сходимость или расходимость которого нам известна, и если начиная с некоторого номера
1) 
и ряд 
сходится, то ряд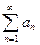 
также сходится;
2). 
и ряд расходится, то ряд 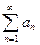также расходится.
При использовании этого признака исследуемый ряд чаще всего сравнивается либо с бесконечной геометрической прогрессией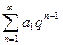 
, либо с обобщенными гармоническими рядами 
, поведение которых в смысле сходимости мы обсудили выше.
Заметим, что признак Даламбера является, по сути, признаком сравнения с подходящей геометрической прогрессией, правда сама прогрессия не подбирается при непосредственном применении признака Даламбера – это большое его достоинство.
Задача №8.Исследовать на сходимость ряд 
.
Решение. Сравним данный ряд с обобщенным гармоническим рядом 
.
Каждый член 
данного ряда, начиная с 
, не больше соответствующего члена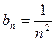 
обобщенного гармонического ряда:
,
и поскольку ряд сходится ( 
), то согласно утверждению 1) первого признака сравнения исследуемый ряд также сходится.
Ответ: ряд сходится.
Задача №9.Исследовать на сходимость ряд 
.
Решение. Докажем, что данный ряд расходится. Для этого используем утверждение 2) первого признака сравнения и подбирем расходящийся ряд с меньшими членами:
, 
,
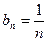Поскольку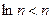 
для всех натуральных 
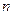, то
.
Гармонический ряд 
расходится, следовательно, по признаку сравнения ряд также расходится.
Ответ: ряд расходится.
Задача №10.Исследовать ряд на сходимость 
.
Решение. Главная особенность использования признака сравнения состоит в том, что здесь, в отличие от других достаточных признаков сходимости, необходимо делать предположение о том, сходится ряд или расходится. Докажем сходимость данного ряда. Для этого докажем, что, начиная с некоторого номера 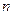, верно соотношение
.
Применяя правило Лопиталя (дифференцирование по 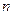) получим
значит, начиная с некоторого 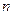, функция 
меньше 
для любого 
.
Положим 
, тогда
, откуда имеем
.
, 
.
Обобщенный гармонический ряд 
сходится ( 
), следовательно, по признаку сравнения ряд с меньшими членами также сходится.
Ответ: ряд сходится.
Сформулируем второй признак сравнения.
Теорема 2. (второй признак сравнения рядов с положительными членами).
Пусть даны два ряда 
и 
. Если предел отношения общих членов этих рядов 
существует, конечен и не равен нулю, то ряды одновременно сходятся или расходятся.
Задача №11. Исследовать на сходимость ряд 
.
Решение. Попытаемся сравнить наш ряд с обобщенным гармоническим. Обсудим сначала, каким образом в этом случае подобрать обобщенный гармонический ряд. Очевидно, что главными в числителе и в знаменателе являются слагаемые, содержащие старшие степени переменной 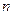, именно их и оставим при подборе гармонического ряда:
.
Обозначим 
, .
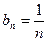Вычислим предел, который подтверждает, что ряды сходятся или расходятся одновременно:
.
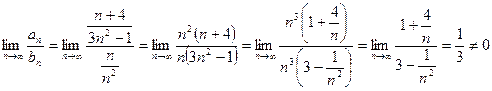Ряд 
расходится как гармонический.
Следовательно, по второму признаку сравнения исходный ряд также расходится.
Ответ: ряд расходится.
Задача №12.Исследовать на сходимость ряд 
.
Решение. Сравним данный ряд с рядом 
.
Обозначим
, 
, тогда
.
Ряд 
состоит из членов бесконечно убывающей геометрической прогрессии 
и, следовательно, сходится. По обобщенному признаку сравнения сходится и исследуемый ряд.
Ответ: ряд сходится.
Задача №13. Исследовать на сходимость ряд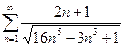 
.
Решение. Сравним данный ряд с обобщенным гармоническим рядом (при подборе ряда для сравнения мы оставляем старшие степени 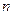в числителе и знаменателе):
.
Обозначим 
, 
.
Вычислим предел
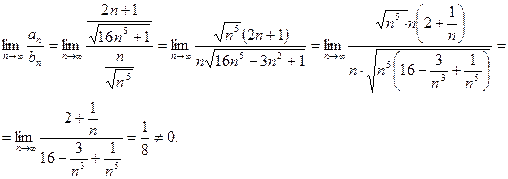
Следовательно, ряды в смысле сходимости ведут себя одинаково.
Ряд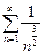 
сходится, поскольку является обобщенным гармоническим, 
. Тогда по второму признаку сравнения исходный ряд также сходится.
Ответ: ряд сходится.
Задача №14.Исследовать на сходимость ряд 
.
Решение. Подберем данному ряду обобщенный гармонический ряд так, чтобы ряды сходились или расходились одновременно (учтём, что тангенс малого угла примерно равен самому углу – это следствие первого замечательного предела):
.
Обозначим 
, 
, тогда
Здесь использовалась формула
.
Обобщенный гармонический ряд 
расходится, 
. Используя второй признак сравнения, делаем вывод о том, что исходный ряд расходится.
Ответ: ряд расходится.