Здавалка
Главная | Обратная связь

Дифференциал функции.

⇐ ПредыдущаяСтр 10 из 14Следующая ⇒

1. Приращение ∆у дифференцируемой функции у=f(x) может быть представлено в виде:

∆у= f'(x) ∆x + a (∆x) ∆x, где ∆x- приращение независимой переменной.

2. Дифференциалом функции у=f(x) называется главная, линейная относительно ∆x часть приращения функции, равная произведению производной на приращение независимой переменной:

Dy= f'(x) ∆x/

Дифференциал независимой переменной равен приращению этой переменной: dx=∆x/

Свойства дифференциала:

1. dc=0, c- const.

2. d(u±v)=du±dv.

3. d(u/v)=vdu-udv/v2.

4. d(cu)=c du.

5. d(uv)=v du + u dv.

6. dy=f'(u)du.

 

 

Семинар№9. Методы интегрирования неопределенного интеграла.

Приложения определенного интеграла.

ПЗ №9. Интегральное исчисление.

1. Разбор домашнего задания №8

2. Найти неопределенные интегралы:

; 2) ; 3) ; 4) .

Неопределенный интеграл.

1. Функция F(х) называется первообразной для функции f(х) на промежутке Х, если в каждой точке х этого промежутка справедливо равенство F'(x)=f(x).

Совокупность всех первообразных для функцииf(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается

∫ f(x)dx:

∫f(x)dx=F(x)+C

f(x)-подынтегральная функция, f(x)dx-подынтегральное выражение, С-произвольная постоянная.

Нахождение неопределенного интеграла называется интегрированием.Операции интегрирования и дифференцирования являются взаимно обратными.

Свойства интеграла:

1. ∫d([f(x)dx)= f(x)dx

2. ∫dF(x)=F(x)+C

3. ∫af(x)dx=a[f(x)dx

4. ∫ (f(x)±g(x))dx=∫f(x)dx±∫g(x)dx.

Табличные интегралы.

1. ∫0dx=C

2. ∫xndx=xn+1/n+1

3. ∫dx/x=lnx+C

4. ∫axdx=ax/ln a+C

5. ∫exdx=ex+C

6. ∫sin x dx= - cos x+C

7. ∫cos xdx=sinx+C

8. ∫dx/cos2x=tg x+C

9. ∫dx/sin2x=-ctg x+C

10. ∫dx /(a2+x2 )=1/a arctg x/a +C

11. ∫dx/x2-a2 =1/2a ln│x-a/x+a│+C

Метод замены переменной.

Пусть х=ω(t)-непрерывно дифференцируема на рассматриваемом промежутке. Тогда [f(x)dx=[f(ω(t))ω'(t)dt.

Формула интегрирования по частям. ∫u dv=uv-∫v du.

Семинар№10.

ПЗ№10.5) Найти площадь фигуры, ограниченной линиями y2=9x и y=3x.

6) Найти площадь фигуры, ограниченной равнобочной гиперболой xy=4 и прямой x+y=5.

7) Определить длину половины окружности x2+y2=9.

Семинар№11.

ПЗ №11. Дифференциальные уравнения.

1. Разбор домашнего задания №10

2. Найти общее решение: 1) ; 2) ; 3)

Решите задачу Коши: 1) ;

2)

 

Семинар№12. ПЗ №12. Ряды. Числовые ряды.

1. Разбор домашнего задания №11

2. 1) Найти общий член ряда: ;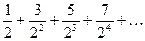

2) Найти сумму ряда: ;

3) Исследовать сходимость ряда: ;

4) Исследовать сходимость ряда: ;

5) Исследовать сходимость ряда: .

Семинар№13.

ПЗ №13. Введение в теорию вероятностей.

1. Разбор домашнего задания №12

2. 1) Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна семи.

2) В ящике содержится 10 одинаковых деталей, помеченных номерами 1, 2, ..., 10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажется деталь №1.

3) В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.

4) Вероятность успешной попытки выполнить упражнение для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди. Причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.

5) Отрезок АВ длиною 15 см разделен точкой С в отношении 2:1. На этот отрезок наудачу брошены 4 точки. Найти вероятность того, что две из них окажутся левее точки С и две-правее. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависист от его расположения.

6) Дискретная случайная величина Х задана законом распределения:

а) Х 2 4 5 6

Р 0,3 0,1 0,2 0,4

б) Х 10 15 20

Р 0,1 0,7 0,2.

Построить многоугольник распределения.

7) Найти математическое ожидание дискретной случайной величины Х, заданной законом распределения:

Х -4 6 10

р 0,2 0,3 0,5.

Семинар№14.

ПЗ №14. Теория вероятностей.

1. Разбор домашнего задания №13

2. 1) Двумерная случайная величина (X,Y) имеет плотность вероятности: . Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми х=0, х=1, у=0, у=1.

2) Система двух случайных величин (X,Y) равномерно распределена в треугольнике, ограниченном прямыми у=х, у=5, х=5. Найти: а) МX, МY, DX, DY; б) коэффициент корреляции .

3) Определить плотность вероятности ситемы двух положительных случайных величин X,Y по заданной функции распределения: .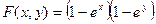

4) Случайные величины X и Y независимы и нормально распределены с MX=MY=0, DX=DY=25. Найти вероятность того, что случайная точка (X,Y) попадет в кольцо: .

5) В механическом цехе работают К токарей. Вероятность того, что токарю потребуется резец данного типа, равна p. Сколько резцов данного типа должна иметь инструментальная кладовая, чтобы потребность в них была обеспечена с вероятностью 0,95?

6) Нарисуйте граф состояний для марковской цепи, вероятности перехода которой заданы матрицей .

Семинар№15.

ПЗ №15. Математическая статистика.

1. Разбор домашнего задания №14

2. 1) Найти эмпирическую функцию по данному распределению выборки:

xi 1 4 6

ni 10 15 25.

2) Построить полигон частот по данному распределению выборки:

xi 1 4 5 7

ni 20 10 14 6.

3) Из генеральной совокупности извлечена выборка объема n=60:

варианта xi 1 3 6 26

частота ni 8 40 10 2.

Найти несмещенную оценку генеральной совокупности.

4) Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратичное отклонение σ=5, выборочная средняя 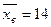и объем выборки n=25.

5) Найти коэффициент линейной корреляции между признаками Х и Y и написать уравнения прямых регрессии для корреляционной таблицы признаков:

X/Y Ni*
       
       
     
     
     
Nj*

 

Задания на СРСП.

СРСП №1. 1). Вычислить определитель матрицы А (табл. 4).

2). Найти произведение матриц А и В: (табл. 5).

,

3). Дана матрица А (табл. 6). Найти матрицу А-1 и установить,

что А А-1 =Е.

СРСП № 2. Найти общее решение системы линейных уравнений (табл. 7) методом Гаусса.

СРСП №3-4. 1) Дан параллелограмм АВСД, три вершины которого заданы (табл. 1). Найти четвертую вершину и острый угол параллелограмма.

2) Найти длину высоты АД в треугольнике с вершинами А, В, С (табл. 2) и написать уравнение перпендикуляра, опущенного из точки С на прямую АВ.

3).Построить кривые по заданным уравнениям (табл. 3).

СРСП № 5-6. Вычислить предел (табл. 9).

СРСП №7. Исследовать функцию (табл. 10) и построить ее график.

СРСП №8. Найти частные производные второго порядка функции многих переменных (табл. 11).

СРСП №9. Найти неопределенный интеграл (табл. 12).

СРСП №10. Вычислить определенный интеграл (табл. 13).

1) Вычислить площадь фигуры, ограниченной линиями (табл. 14).

2) Вычислить несобственный интеграл (табл. 15).

СРСП №11. Решить дифференциальное уравнение первого порядка (табл. 16).

СРСП № 12. Найти промежуток сходимости степенного ряда (табл. 17).

СРСП №13. 1) В партии из N изделий n изделий имеют скрытый дефект (табл. 18). Каковавероятность того, что из взятых наугад m изделий k изделий являются дефектными?

3) В магазине выставлены для продажи n изделий, среди которых k изделий некачественные (табл. 19). Какова вероятность того, что взятые случайным образом m изделий будут некачественными?

СРСП №14. На сборочное предприятие поступили однотипные комплектующие стрех заводов в количестве: n1 с первого завода, n2 со второго, n3 с третьего (табл. 20). Вероятность качественного изготовления изделий на первом заводе p1, на втором p2, на третьем p3. Какова вероятность того, что взятое случайным образом изделие будет качественным?

СРСП № 15. Дано распределение дискретной случайной величины X (табл. 21). Найти математическое ожидание и среднее квадратичное отклонение.

 

(Вариант соответствует порядковому номеру студента в списке)

Таблица № 1

Вари ант А В С Вари ант А В С
1. (-1;-2;3) (-4;1;2) (5;2;7) 16. (-3;5;-4) (-5;6;2) (3;-5;-2)
2. (1;2;3) (3;-4;-2) (-4;-3;2) 17. (2;-3;4) (6;-4;-5) (-3;4;-2)
3. (2;-3;-1) (-3;5;3) (4;3;-4) 18. (5;-2;-4) (-5;-8;-1) (-2;4;3)
4. (3;-4;2) (-5;2;-3) (-1;7;-2) 19. (-3;-2;-5) (-4;-5;3) (2;3;4)
5. (-5;2;4) (-3;-4;2) (6;-3;-3) 20. (2;6;-3) (-5;-2;-4) (-3;-5;1)
6. (-4;-3;5) (2;-5;6) (-2;3;-5) 21. (3;-1;-2) (2;-4;1) (7;5;2)
7. (4;2;-3) (-5;6;-4) (-2;-3;4) 22. (3;1;2) (-2;3;-4) (2;-4;-3)
8. (-4;5;-2) (-1;-5;-8) (3;-2;4) 23. (-1;2;-3) (3;-3;5) (-4;4;3)
9. (-5;-3;-2) (3;-4;-5) (4;2;3) 24. (2;3;-4) (-3;-5;2) (-2;-1;7)
10. (-3;2;6) (-4;-5;-2) (1;-3;-5) 25. (4;-5;2) (2;-3;-4) (-3;6;-3)
11. (-2;3;-1) (1;2;-4) (2;7;5) 26. (5;-4;-3) (6;2;-5) (-5;-2;3)
12. (2;3;1) (-4;-2;3) (-3;2;-4) 27. (-3;4;2) (-4;-5;6) (4;-2;-3)
13. (-3;-1;2) (5;3;-3) (3;-4;4) 28. (-2;-4;5) (-8;-1;-5) (4;3;-2)
14. (-4;2;3) (2;-3;-5) (7;-2;-1) 29. (-2;-5;-3) (-5;3;-4) (3;4;2)
15. (2;4;-5) (-4;2;-3) (-3;-3;6) 30. (6;-3;2) (-2;-4;-5) (-5;1;-3)

Таблица № 2

Вариант А В С Вариант А В С
1. (3;4) (2;-1) (1;7) 16. (3;2) (2;-5) (-6;-1)
2. (-4;-5) (3;3) (5;-2) 17. (6;-4) (-3;-7) (-1;2)
3. (-3;5) (4;-3) (-2;-4) 18. (-2;-1) (7;3) (4;-3)
4. (3;-2) (-5;-4) (-1;6) 19. (3;4) (6;7) (1;1)
5. (2;5) (-3;4) (-4;-2) 20. (-4;-5) (-2;2) (-7;4)
6. (-3;2) (-2;-5) (6;-1) 21. (3;-4) (2;1) (1;7)
7. (-6;-4) (3;-7) (1;2) 22. (-4;5) (3;-3) (5;2)
8. (2;1) (-7;3) (-4;-3) 23. (-3;-5) (4;3) (-2;4)
9. (-3;-4) (-6;7) (-1;1) 24. (3;2) (-5;4) (-1;-6)
10. (4;-5) (2;2) (7;4) 25. (2;-5) (-3;-4) (-4;2)
11. (-3;4) (-2;-1) (-1;-7) 26. (-3;-2) (-2;5) (6;1)
12. (4;-5) (-3;3) (-5;-2) 27. (-6;4) (3;7) (1;-2)
13. (3;5) (-4;-3) (2;-4) 28. (2;1) (-7;-3) (-4;3)
14. (-3;-2) (5;-4) (1;6) 29. (-3;4) (-6;-7) (-1;-1)
15. (-2;5) (3;4) (4;-2) 30. (4;5) (2;-2) (7;-4)

Таблица № 3

Вариант Уравнения Вариант Уравнения
1. 16.
2. 17.
3. 18.
4. 19.
5. 20.
6. 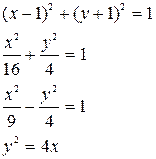21.
7. 22.
8. 23.
9. 24.
10. 25.
11. 26.
12. 27.
13. 28.
14. 29.
15. 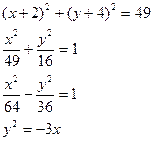30.


Таблица № 4

Вариант Матрица А Вариант Матрица А
1. 16.
2. 17.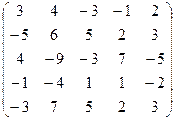
3. 18.
4. 19.
5. 20.
6. 21.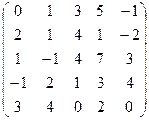
7. 22.
8. 23.
9. 24.
10. 25.
11. 26.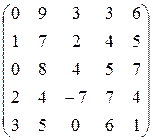
12. 27.
13. 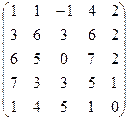28.
14. 29.
15. 30.

Таблица № 5

Вариант K1 K2 K3 Вариант K1 K2 K3
1. -5 -3 2. -2
3. -3 4.
5. -2 6.
7. -3 8.
9. -2 10.
11. -4 -3 12.
13. -1 -2 14. -3 -4
15. -4 16. -4
17. -5 18.
19. -3 20. -4
21. -1 22.
23. -1 24. -1
25. -4 26. -1
27. -3 28.
29. 30. -3 -1

Таблица № 6

Вариант Матрица А Вариант Матрица А
1.
2.
3.
4.
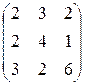
5.
6.
7.
8.
9.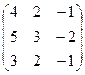
10.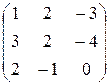
11.
12.
13.
14.
15.


Таблица № 7

Вариант Система уравнений Вариант Система уравнений
1.
2.
3.
4.  
5.
6.
7.
8.
9.
10.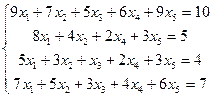
11.
12.
13.
14.
15.

 

Таблица № 8

Вариант Матрица Вариант Матрица
1. 16.
2. 17.
3. 18.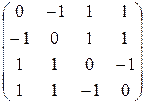
4. 19.
5. 20.
6. 21.
7. 22.
8. 23.
9. 24.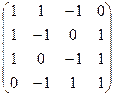
10. 25.
11. 26.
12. 27.
13. 28.
14. 29.
15. 30.

Таблица № 9

Вариант Предел Вариант Предел
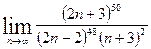
16.
17.
18.
19.
20.
21.
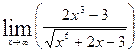
22.
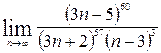
23.
24.
25.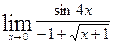
26.
27.
28.
29.
30.

 

Таблица № 10

Вариант Функция Вариант Функция

 

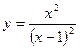
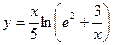
Таблица № 11

Вариант Функция Вариант Функция

 

 

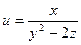
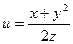
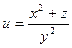
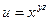
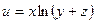
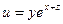
Таблица № 12

Вариант Интеграл Вариант Интеграл
 

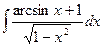
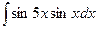
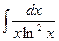
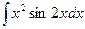
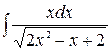
Таблица № 13

Вариант Интеграл Вариант Интеграл
1. 16.
2. 17.
3. 18.
4. 19.
5. 20.
6. 21.
7. 22.
8. 23.
9. 24.
10. 25.
11. 26.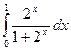
12. 27.
13. 28.
14. 29.
15. 30.

Таблица № 14

Вариант Уравнения линий Вариант Уравнения линий
1. 16.
2. 17.
3. 18.
4. 19.
5. 20.
6. 21.
7. 22.
8. 23.
9. 24.
10. 25.
11. 26.
12. 27.
13. 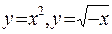28.
14. 29.
15. 30. ⇐ Предыдущая567891011121314Следующая ⇒





©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.