 |
|
Зачетное задание №5 Дифференциальные уравнения

Справочный материал
Дифференциальные уравнения первого порядка.
| № п/п | Некоторые дифференциальные уравнения первого порядка | Подстановка, приводящая к уравнениям с разделяющимися переменными | |
| 1. | Уравнения с разделяющимися переменными | f(x)dx+ g(y)dy=0 | |
| Однородные уравнения | 
| 
| |
| Линейные уравнения | 
| 
| |
| Уравнения Бернулли | 
| 
|
Структура общего решения однородного дифференциального уравнения с постоянными коэффициентами : 
Характеристическое уравнение: 
| ||
| № п/п | Вид корней характеристического уравнения | Фундаментальная система частных решений |
Корни характеристического уравнения действительные различные

| 
| |
Корни характеристического уравнения различные, среди них имеются комплексно-сопряженные

| 
| |
Корень характеристического уравнения  - корень кратности «к» - корень кратности «к»
| 
| |
| Общее решение | ||

|
Структура частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами и специальной правой частью:
 ,f(x) =
,f(x) =  (
(  )
)

| Вид правой части | Проверяемое зна-чение корня характе-ристического уравн. 
| Вид частного решения, если  не является корнем характеристического уравнения не является корнем характеристического уравнения
| Вид частного решения, если  -корень кратности характеристического уравнения -корень кратности характеристического уравнения
|

|  =0 =0
| 
|  
|
 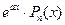
|  =а =а
| 
|  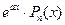
|

|  = = 
| 
|  ( (  ) )
|
 ( (  ) )
|  =а =а 
|  ( (  ) )
|   ( (  ) )
|
Задания для самостоятельной работы
Задание 1. Найти решения дифференциальных уравнений первого порядка.
| 1. | а)  в)
в) 
|
| 2. | а)  в)
в) 
|
| 3. | а)  в)
в) 
|
| 4. | а)  в)
в) 
|
| 5. | а)  в)
в) 
|
| 6. | а)  в)
в) 
|
| 7. | а)  в)
в) 
|
| 8. | а)  в)
в) 
|
| 9. | а)  в)
в) 
|
| 10. | а) 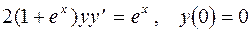 в)
в) 
|
| 11. | а)  в)
в) 
|
| 12. | а)  в)
в) 
|
| 13. | а)  в)
в) 
|
| 14. | а)  в)
в) 
|
| 15. | а)  в)
в) 
|
| 16. | а)  в)
в) 
|
| 17. | а) 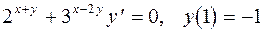 в)
в) 
|
| 18. | а)  в)
в) 
|
| 19. | а)  в)
в) 
|
| 20. | а) 
 в) в) 
|
а)  в)
в) 
| |
а)  в)
в) 
| |
а)  в)
в) 
| |
а)  в)
в) 
| |
а)  в)
в) 
|
Задание 2. Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка:
1. а)  б)
б)  в)
в) 
| 2. а)  б)
б)  в)
в) 
|
3. а)  б)
б)  в)
в) 
| 4. а)  б)
б) 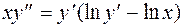 в)
в) 
|
5. а)  б)
б)  в)
в) 
| 6. а)  б)
б)  в)
в) 
|
7. а)  б)
б)  в)
в) 
| 8. а) 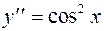 б)
б)  в)
в) 
|
9. а)  б)
б)  в)
в) 
| 10. а)  б)
б)  в)
в) 
|
11. а)  б)
б)  в)
в) 
| 12. а)  б)
б)  в)
в) 
|
13. а)  б)
б)  в)
в) 
| 14. а)  б)
б)  в)
в) 
|
15. а)  б)
б)  в)
в) 
| 16. а)  б)
б)  в)
в) 
|
17. а)  б)
б)  в)
в) 
| 18. а)  б)
б)  в)
в) 
|
13. а)  б)
б)  в)
в) 
| 14. а)  б)
б)  в)
в) 
|
Задание 3. Решить задачу Коши:
1. 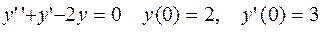
2. 
3. 
4. 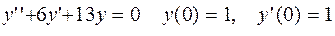
5. 
6. 
7. 

8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Задание 4. Решить линейное неоднородное дифференциальное уравнение:
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 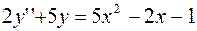
| 14. 
|
15. 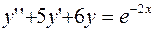
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задание 5. Решить систему дифференциальных уравнений:
1. 
| 2. 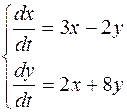
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 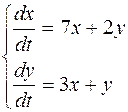
|
17. 
| 18. 
|
19. 
| 20. 
|
Зачетное задание №6. Числовые и функциональные ряды