 |
|
Зачетное задание №3 Дифференцирование и интегрирование функции нескольких переменных
Справочный материал.
Производная неявной функции.
|  .
 ,  .
|
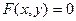
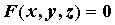
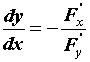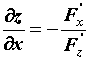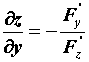Производная по направлению
| 
где  - направляющие косинусы вектора  .
|
Градиент.
| 
|
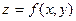
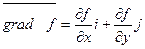
Задания для самостоятельной работы.
Задание1.Дана функция Z=f(x,y). Найти частные производные 1 и 2 порядка.
| 1.1. |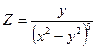 
| 1.2. |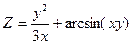 
|
| 1.3. | 
| 1.4. |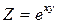 
|
| 1.5. | 
| 1.6. |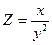 
|
| 1.7. | 
| 1.8. |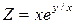 
|
| 1.1. |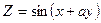 
| 1.10. |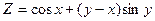 
|
| 1.11. |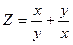 
| 1.12. |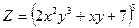 
|
| 1.13. |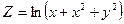 
| 1.14. | 
|
| 1.15. |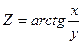 
| 1.16. | 
|
| 1.17. | 
| 1.18. | 
|
| 1.19. |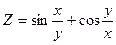 
| 1.20. |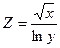 
|
Задание 2.Найти наибольшее и наименьшее значение функции в замкнутой области Д.
| 2.1. | Z = |  ,
| 
|
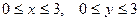
| 2.2. | Z = | 
| 
|
| 2.3. | Z = |  ,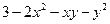
| 
|
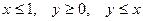
| 2.4. | Z = |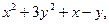 
| 
|
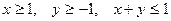
| 2.5. | Z = |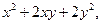 
| 
|
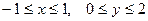
| 2.6. | Z = | 
| 
|
| 2.7. | Z = | 
| 
|
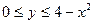
| 2.8. | Z = |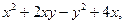 
| 
|
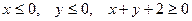
| 2.9. | Z = |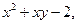 
| 
|
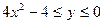
| 2.2. | Z = |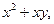 
| 
|
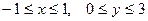
| 2.11. | Z = |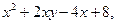 
| 
|
| 2.12. | Z = | 
| 
|
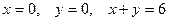
| 2.13. | Z = |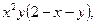 
| 
|
| 2.14. | Z = | 
| 
|
| 2.15. | Z = |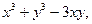 
| 
|
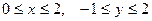
| 2.16. | Z = |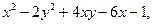 
| 
|
| 2.17. | Z = |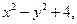 
| 
|
| 2.18. | Z = |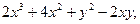 
| 
|
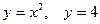
| 2.19. | Z = | 
| 
|
| 2.20. | Z = |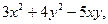 
| 
|
Задание 3.Даны функция Z=Z(x,y), точка А(х0,у0) и вектор 
. Найти:
1) grad Z в точке А;
2) производную в точке А по направлению вектора .
| 3.1. | Z = | 
| А(1,1), |  =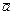
| 
|
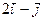
| 3.2. | Z = | 
| А(2,1), | =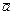
| 
|
| 3.3. | Z = |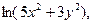 
| А(1,1), | =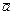
| 
|
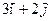
| 3.4. | Z = |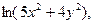 
| А(1,1), | =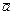
|
|
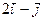
| 3.5. | Z = | 
| А(2,1), | =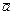
| 
|
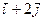
| 3.6. | Z = |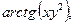 
| А(2,3), | =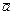
| 
|
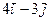
| 3.7. | Z = | 
| А(1,2), |
=
|
|
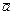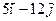
| 3.8. | Z = | 
| А(1,3), | =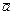
|
|
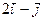
| 3.9. | Z = |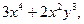 
| А(-1,2), | =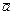
|
|
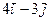
| 3.2. | Z = | 
| А(1,1), | =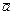
| 
|
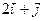
| 3.3. | Z = |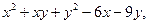 
| А(1,1), | =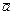
| 
|
| 3.12. | Z = | 
| А(2,3), | =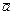
| 
|
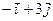
| 3.13. | Z = |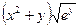 
| А(2,1), | =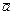
| 
|
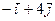
| 3.14. | Z = |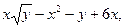 
| А(3,2), | =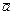
| 
|
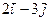
| 3.15. | Z = |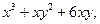 
| А(1,1), | =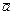
| 
|
| 3.16. | Z = |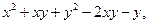 
| А(1,3), | =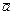
| 
|
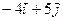
| 3.17. | Z = | 
| А(1,4), | =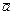
| 
|
| 3.18. | Z = |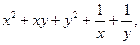 
| А(1,1), |
=
|
|
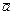| 3.19. | Z = |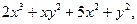 
| А(2,1), | =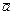
| 
|
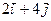
| 3.20. | Z = |  ,
| А(2,2), | =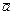
| 
|
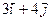
Задание 4. Изменить порядок интегрирования.
1.1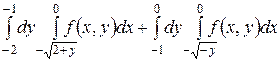 
.
1.2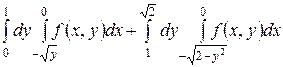 
.
1.3 
.
1.4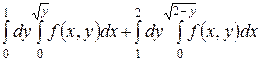 
.
1.5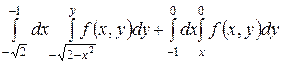 
.
1.6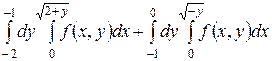 
.
1.7 
.
1.8.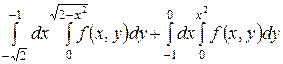 
.
1.9 
.
1.10 
.
1.11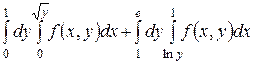 
.
1.12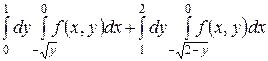 
.
1.13 
.
1.14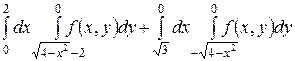 
.
1.15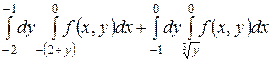 
.
1.16 
.
1.17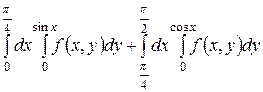 
.
1.18 
.
1.19 
.
1.20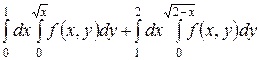 
.
Задание 5. Вычислить двойной интеграл.
2.1 
.
2.2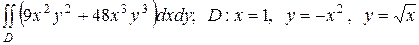 
.
2.3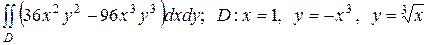 
.
2.4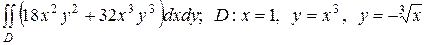 
.
2.5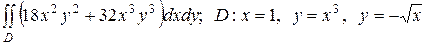 
.
2.6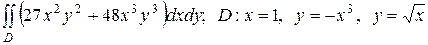 
.
2.7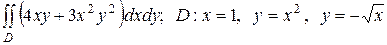 
.
2.8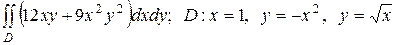 
.
2.9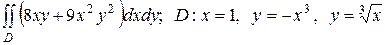 
.
2.10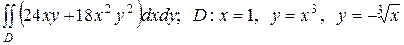 
.
2.11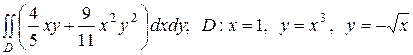 
.
2.12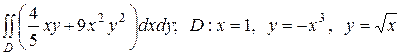 
.
2.13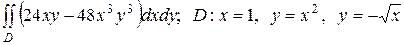 
.
2.14 
.
2.16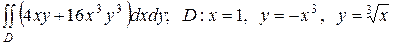 
.
2.17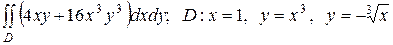 
.
2.18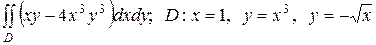 
.
2.19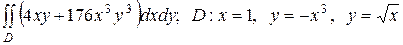 
.
2.20 
.
Задание 6. Найти площадь фигуры, ограниченной данными линиями.
3.1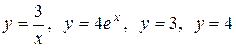 
.
3.2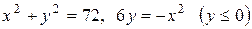 
.
3.3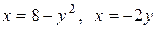 
.
3.4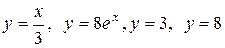 
.
3.5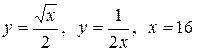 
.
3.6 
.
3.7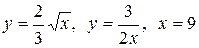 
.
3.8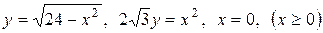 
.
3.9 
.
3.10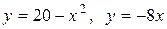 
..
3.11 
.
3.12 
.
3.13 
.
3.14 
.
3.15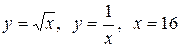 
.
3.16 
.
3.17 
.
3.18 
.
3.19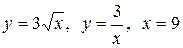 
.
3.20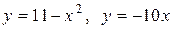 
.
Зачетное задание №4 Интегралы
Справочный материал
НЕОПРЕДЕЛЕННЫй ИНТЕГРАЛ.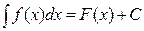 
Основные свойстванеопределенного интеграла.
1). 
;
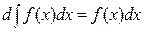2). 
;
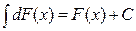3). 
;
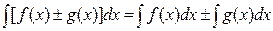4). 
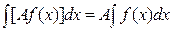, где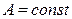 
5) 
- свойство инвариантности
Таблица основных производных и интегралов
| 
| 
| 
|
| 
|
|
|
| 
| 
| 
|
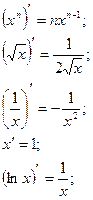
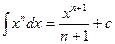
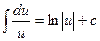
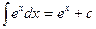
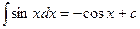
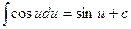
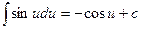
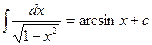
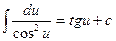
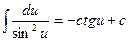
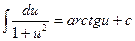
методы интегрирования.
1. Интегрирование подстановкой
.
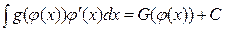2. Интегрирование методом интегрирования по частям
.
Типы интегралов, берущиеся интегрированием по частям:
| |
| |
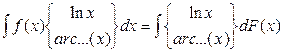
| «круговой интеграл» |  , 
|
Интегрирование рациональных алгебраических функций:
1.Если подынтегральная дробь неправильная, то нужно выделить целую часть.
2. Если дробь правильная, то нужно применить разложение правильной дроби на простейшие дроби:
Интегрирование тригонометрических функций:
1. Используемые формулы:
, 
, 
.
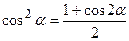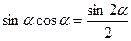Примеры: 
, 
, 
.
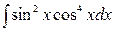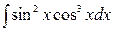2.Используемые формулы:
,
,
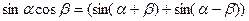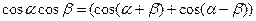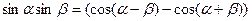
Пример: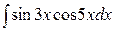 
.
3.Универсальная тригонометрическая подстановка:
- подстановкой 
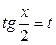, тогда 
,
, 
, 
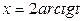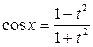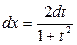
Пример: 
.
4. Если под интегралом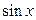 
и 
содержатся только в четных степенях, то лучше применять подстановку:
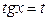, тогда 
, 
, 
, 
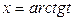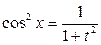5. 
- подстановкой 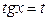, тогда , .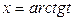