 |
|
Справочный материал.
| ЧИСЛОВЫЕ РЯДЫ | |||||
| Необходимый признак сходимости ряда | Достаточные признаки сходимости рядов с положительными членами | ||||
| Признак сравнения | Предельный признак сравнения | Признак Даламбера | Радикальный признак Коши. | Интегральный признак Коши. | |
Если ряд сходится, то его общий член стремится к нулю при неограниченном возрастании его номера.
 . .
| Пусть даны два положительных ряда  (1) и (1) и 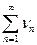 (2), если (2), если 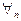  , то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) - расходимость ряда (2). , то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) - расходимость ряда (2).
| Если существует конечный и отличный от нуля предел  , то оба ряда , то оба ряда  и и 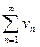 одновременно сходятся или расходятся. одновременно сходятся или расходятся.
| Если существует предел отношения последующего члена ряда к предыдущему 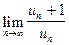 , то при
q < 1 ряд сходится,
q > 1 ряд расходится,
q = 1 признак ответа не дает. , то при
q < 1 ряд сходится,
q > 1 ряд расходится,
q = 1 признак ответа не дает.
| Если существует  , то при q < 1 ряд сходится, при q > 1 ряд расходится, а при q = 1 признак ответа не дает. , то при q < 1 ряд сходится, при q > 1 ряд расходится, а при q = 1 признак ответа не дает.
| Если  при х ³ 1 - непрерывная, положительная и монотонно убывающая функция, то ряд
при х ³ 1 - непрерывная, положительная и монотонно убывающая функция, то ряд  , где , где 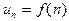 и несобственный интеграл и несобственный интеграл  сходится или расходится одновременно сходится или расходится одновременно
|
| ЧИСЛОВЫЕ ЗНАКОПЕРЕМЕННЫЕ И ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ. | |||||
| Абсолютная сходимость | Условная сходимость | ||||
| Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов | Если ряд, составленный из абсолютных величин членов знакочередующегося ряда расходится, а по признаку Лейбница ряд сходится, то ряд сходится условно. | ||||
Признак Лейбница.Знакочередующийся ряд  сходится, если его члены, взятые по абсолютной величине, монотонно убывают и общий член сходится, если его члены, взятые по абсолютной величине, монотонно убывают и общий член 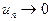 при при  т.е.:
1) т.е.:
1)  2)
2) 
| |||||
| СТЕПЕННЫЕ РЯДЫ | |||||

| Радиус сходимости  .
Областью абсолютной сходимости степенного ряда является (-R; R) .
Областью абсолютной сходимости степенного ряда является (-R; R)
| ||||
| РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В РЯД МАКЛОРЕНА | |||||
1.  2.
2.  3.
3.  4.
4.  5.
5. 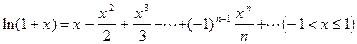 6.
6. 
|
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.