Главная | Обратная связь

Систем линейных уравнений с помощью ранга матрицы

Рассмотрим алгоритм решения системы линейных уравнений и в необходимых местах приведем обоснования.

Дана система линейных уравнений (1).

1. Исследуем ее на совместность. Для этого находим ранги матриц А и .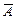

Если они различны, то система несовместна (по теореме Кронекера – Капелли).

Пусть (8). Тогда по той же теореме система (1) совместна.

Если М – базисный минор матрицы А, то из равенств (8) следует, что он имеет порядок r и остается базисным минором матрицы 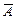. Не нарушая общности, можно считать, что минор М находится в левом верхнем углу 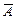(в противном случае можно перенумеровать неизвестные и переставить уравнения). Тогда первые r строк матрицы 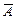являются базисными строками, и потому по теореме о базисном миноре все остальные строки этой матрицы линейно выражаются через первые r строк. Отсюда нетрудно получить, что все уравнения системы (1) линейно выражаются через первые r уравнений этой системы.

Рассмотрим следующую систему уравнений:

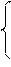a₁₁x₁+…+a_1rx_r+a_1r+1x_r+1+…+a_1nx_n=b₁

…………………………………. (9)

a_r1x₁+…+a_rrx_r+a_rr+1x_r+1+…+a_rnx_n=b_r.

 

В системе (9) мы оставили только те уравнения из (1), коэффициенты из которых входят в минор М.

Докажем, что системы (I) и (9) имеют одно и то же множество решений, т.е. эквивалентны (равносильны).

Очевидно, что всякое решение системы (1) является и решением системы (9), так как (9) – это часть системы (1).

Обратно: всякое решение системы (9) удовлетворяет и остальным уравнениям системы (1), так как «отброшенные» уравнения, как отмечено выше, есть линейные комбинации уравнений (9).

Мы обосновали следующий факт: при решении системы (1) можно отбросить «лишние» уравнения и получить систему r линейно независимых уравнений, эквивалентную (1).

2. Рассмотрим систему (9). Перенесем в ней в правые части все неизвестные, коэффициенты при которых не входят в минор М (в нашем случае – неизвестные x_r+1,…x_n (10)). Эти неизвестные назовем свободными неизвестными.

Придадим свободным неизвестным произвольные значения из поля Р:

x_r+1=c_r+1, …, x_n=c_n (11), c_jÎP, j=r+1,…,n.

Для нахождения остальных неизвестных x₁,…,x_r (их назовем основными), получаем следующую систему уравнений:

 

 

a₁₁x₁+…+a_1rx_r=b₁-a_1r+1c_r+1-…-a_1nc_n

………………………. (12)

a_r1x₁+…+a_rrx_r=b_r-a_rr+1c_r+1-…-a_rnc_n.

 

(12) – система r уравнений с r неизвестными, причем ее определитель – базисный минор М – отличен от нуля (такие системы называют крамеровскими, так как к ним применима теорема Крамера).

По теореме Крамера система (12) имеет единственное решение: x₁=c₁,…, x_r=c_r. (13)

Теперь нетрудно видеть, что c₁,…, c_r, c_r+1,…,c_n (14) (мы объединили наборы чисел (11) и (13)) – это решение системы (9).

В части 2 мы обосновали следующий факт: почему свободным неизвестным можно придавать произвольные значения? Потому, что если это сделать, то мы можем найти некоторое решение системы (1).

В этой же части мы научились находить некоторые решения системы (1).

3. Докажем, что описанным выше способом можно получить любое решение системы (1).

Пусть(c₁,…,c_r,c_r+1,…,c_n) (15) – произвольное решение системы (1). Если x_r+1, …, x_n - свободные неизвестные, то придадим им значения, взятые из решения (15):

x_r+1=c_r+1, …, x_n=c_n. Тогда значения основных неизвестных найдутся по теореме Крамера при решении системы (12):

x₁=d₁,…, x_r=d_r. (16)

Так как (15) – решение системы (1), то система (12) имеет решение x₁=c₁,…,x_r=c_r (17). По теореме Крамера решение системы (12) единственно, и потому ее решения (16) и (17) должны совпадать.

Мы доказали, что произвольное решение (15) системы (1) можно получить описанным выше способом.

Общее решение

Отметим, что общее решение системы линейных уравнений можно получить методом Гаусса: выразить основные неизвестные через свободные. Другой способ получения общего решения вытекает из рассмотренного выше метода решения системы с помощью ранга матрицы. Для этого при решении системы (9) свободные неизвестные переносим в правые части уравнений системы и считаем их произвольными постоянными, т.е. полагаем

x_r+1=С₁,…, x_n=С_n-r. (17)

А далее по формулам Крамера выражаем основные неизвестные через свободные. Получим:

x₁=f₁(С₁,…,C_n-r),…, x_r=f_r(C₁,…,C_n-r). Отметим, что f₁,…,f_r — некоторые линейные функции от С₁,…, С_r. Тогда (f₁,…,f_r, C₁,…, C_n-r) (18) будет, очевидно, решением системы (1).

Это решение содержит произвольные постоянные и, как доказано выше в пункте 3, любое решение системы (1) можно получить при некотором выборе этих произвольных постоянных. Следовательно, (18) – общее решение системы (1).