Главная | Обратная связь

Задание подпространств конечномерных линейных пространств системами линейных однородных уравнений

Определение 10. Будем говорить, что система линейных уравнений с n неизвестными над полем Р задает некоторое подпространство Н n-мерного линейного пространства L над полем Р, если координаты всех векторов из Н в некотором базисе L, и только этих векторов, удовлетворяют этой системе.

Учитывая это определение и доказанные выше теоремы 1 и 2 об однородных системах, нетрудно видеть, что справедливо утверждение:

Теорема 4. Однородная система линейных уравнений ранга r с n неизвестными при r<n задает некоторое (n-r)-мерное подпространство любого n-мерного линейного пространства над полем Р.

Справедлива и обратная теорема.

Теорема 5. Всякое r-мерное подпространство Н n-мерного линейного пространства L над полем Р при r<n может быть задано однородной системой линейных уравнений ранга (n-r), а именно линейно независимой системой из (n-r) уравнений.

Доказательство. Выберем в L какой-нибудь базис e=(e₁,…,e_n), а в Н – базис h=(h₁,…,h_r). Отметим, что H=<h₁,…,h_r>. Найдем координаты векторов базиса h в базисе е (здесь мы будем пользоваться координатными строками):

h₁(a₁₁,…,a_1n),…, h_r(a_r1,…,a_rn). Составим следующую однородную систему:

, i=1,…, r (1)

Ее матрицей будет:

 

A=

.

Так как h – это базис Н, то векторы h₁,…,h_r, а значит и их координатные строки (строки матрицы А) линейно независимы, т.е. ранг матрицы А равен r. В силу следствия 1 теоремы 2 фундаментальная система решений системы (1) состоит из (n-r) решений. Пусть f₁,…,f_n-r (2) – одна из фундаментальных систем решений системы (1). При нахождении фундаментальной системы решений (1) мы получаем векторы f_k, заданные координатами в базисе е: f_k(g_k1,…,g_kn), k=1,2,…,n-r. Составим из этих координатных строк матрицу В=(g_ki). Так как система векторов (2) линейно независима, то ранг В равен n-r.

Из того, что векторы f_k являются решениями системы (1), вытекает справедливость тождеств:

(для каждого i=1,…,n)

 

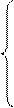............... (3)

.

 

А теперь применим следующую “хитрость”: заменим в (3) числа a_i1,…., a_in, соответственно, неизвестными x₁,…, x_n. Получим однородную систему линейных уравнений:

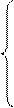............... (4)

.

 

Матрицей системы является матрица В, ее ранг равен (n-r) (и потому уравнения системы (4) линейно независимы). По теореме 4 система (4) задает в L подпространство S размерности n-(n-r)=r. В силу равенств (3) (для любого i) системе (4) удовлетворяют координаты векторов h₁(a₁₁,…,a_1n),…, h_r(a_r1,…,a_rn), т.е. h_jÎS. Но система векторов h₁,…,h_r линейно независима, а dim S = r. Значит, h₁,…,h_r – базис S и S=<h₁,…,h_r>. Учитывая, что H=<h₁,…,h_r>, получаем: S=H. Итак, система (4) задает подпространство Н.

Теорема доказана.

Замечание 1. Из способа доказательства теоремы 5 виден практический метод нахождения систем однородных уравнений, задающих подпространство Н.

Замечание 2. Задание подпространств однородными системами линейных уравнений удобно использовать для нахождения пересечения подпространств.