Главная | Обратная связь

Критерий совместности системы линейных уравнений

Пусть

a₁₁x₁+…+a_1nx_n=b₁

………………….. (1) – система линейных уравнений над

полем Р,

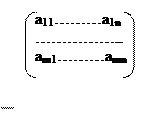a_m1x₁+…+a_mnx_n=b_m т.е. a_ij, b_j ÎP.

 

 

Матрицу А= будем называть матрицей

системы (1).

 

 

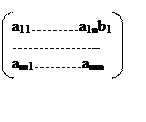
Матрицу А = назовем расширенной

b_m матрицей системы (1).

Теорема Кронекера – Капелли.Система (1) совместна тогда и только тогда, когда матрицы 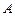и 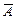имеют одинаковые ранги.

Необходимость. Пусть система (1) совместна. Столбцы матриц 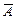и 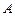будем рассматривать как m-мерные векторы-столбцы. Обозначим систему столбцов матрицы 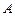через c₁,…c_n (2), матрицы 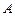– через c₁,…c_n, b (3) (здесь b – столбец свободных членов). Если докажем, что системы векторов (2) и (3) эквивалентны, то отсюда будет следовать, что их ранги равны.

Каждый вектор c_i из (2) содержится в (3) и потому c_i=0×c₁+0×c₂+…+1×c_i+…+0×c_n для любого i. Это означает, что система (2) линейно выражается через систему (3).

Докажем, что система (3) линейно выражается через систему (2). Так как все векторы, кроме b, в этих системах одинаковы, то, в силу отмеченного выше равенства, достаточно доказать, что вектор b линейно выражается через (2). По условию система линейных уравнений (1) имеет решение (k₁,k₁,…,k_n), k_iÎP, т.е. справедливы тождества:

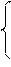a₁₁k₁+…+a_1nk_n=b₁

…………………..

(4)

a_m1k₁+…+a_mnk_n=b_m

 

Из (4) следует, что b=k₁c₁+…+k_nc_n. Это значит, что вектор b линейно выражается через (2), т.е. (3) линейно выражается через (2).

Этим доказано, что системы (2) и (3) эквивалентны. Так как конечные эквивалентные системы векторов имеют одинаковые ранги (по следствию 4 из основной теоремы о линейной зависимости), то ранг системы (2) равен рангу системы (3). Это означает, что ранг матрицы 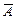равен рангу матрицы .

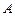Необходимость доказана.

Достаточность. Пусть ранги матрицы 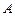и 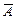совпадают и равны r. Нужно доказать, что система уравнений (1) совместна.

Выберем в системе векторов (2) некоторый базис c_i1,…,c_ir (5). Векторы (5) содержатся в системе (3) и составляют линейно независимую подсистему из r векторов. Так как в силу условия ранг системы (5) также равен r, то (5) будет базисом и системы (3).

Вектор b можно линейно выразить через этот базис, а тогда b линейно выражается и через всю систему (2) (векторы, не входящие в (5), можно добавить в выражение для b с нулевыми коэффициентами).

Мы доказали, что существуют числа k₁,k₂,…,k_n (6) из поля Р такие, что b=k₁c₁+…+k_nc_n (7). Равенство (7) означает, что набор (6) — это решение системы уравнений (1), и потому система (1) совместна.

Теорема доказана.

Определение 7. Рангом совместной системы линейных уравнений называют ранг матрицы этой системы.

Замечание 1.Нетрудно видеть, что для вычисления ранга матрицы 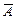достаточно рассмотреть базисный минор М матрицы А и окаймлять его в матрице 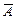только столбцом свободных членов и всеми строками этой матрицы.

Замечание 2.Нетрудно видеть, что если 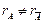, то .

Замечание 3. Отметим, что из способа доказательства теоремы Кронекера – Капелли видно, что если система уравнений (1) совместна и r<n, то эта система имеет решение, в котором (n-r) неизвестных равны 0.