Главная | Обратная связь

Однородные системы и их пространства решений

Определение 8. Система линейных уравнений (1) называется однородной, если b₁=b₂=…=b_m=0.

Таким образом, однородная система линейных уравнений имеет вид:

 

a₁₁x₁+…+a_1nx_n=0

……………… a_ijÎP. (II)

a_m1x₁+…+a_mnx_n=0

 

Однородная система всегда совместна, так как всегда имеет нулевое решение (0,…,0). Поэтому основным вопросом здесь является следующий: существует ли у такой системы хотя бы одно ненулевое решение?

Из приведенных выше критериев для однородной системы получаем:

Основные критерии:

А₀) Нет свободных неизвестных – только нулевое решение;

Б₀) Есть хотя бы одно свободное неизвестное – существует ненулевое решение;

Другие критерии:

1₀) r=n – только нулевое решение;

2₀) r<n – существует ненулевое решение;

3₀) m<n –существует ненулевое решение;

4₀) m=n, d¹0 – только нулевое решение;

5₀) m=n, d=0 – существует ненулевое решение.

Если задана однородная система (II) над полем Р, то любое решение этой системы можно рассматривать как n-мерный вектор-строку:

(b₁,…,b_n)=b, bÎP⁽ⁿ⁾, (b_iÎP).

Докажем некоторые свойства решений однородной системы.

1. Если a=(a₁,…,a_n), b=(b₁,…,b_n) – два решения однородной системы (II), то вектор (a+b)=(a₁+b₁,…,a_n+b_n) также является решением системы (II).

Доказательство. Имеем: так как а и b – решения системы (II), то справедливы следующие равенства: 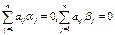. Сложив эти равенства, получим:

. Значит, a+b – тоже решение (II).

2. Пусть а=(a₁,…,a_n) – решение системы (II) и с – некоторое число или произвольное постоянное. Тогда са=(сa₁,…,сa_n) – тоже решение (II).

Доказательство. Имеем: .

Из первого и второго свойств вытекает:

3. Если a₁,…,a_s – некоторые решения системы (II), c₁,…,c_s – числа из Р или произвольные постоянные, то c₁a₁+…+c_sa_s – решение системы (II).

Из свойств 1 и 2 следует

Теорема 1. Множество М всех решений однородной системы (II) над полем Р является подпространством арифметического пространства Р⁽ⁿ⁾.

Доказательство. Действительно, MÌP⁽ⁿ⁾. Пусть a, bÎM: тогда (a+b)ÎM - по первому свойству решений однородной системы.

Для любого aÎР и для любого аÎМ имеем: aаÎМ – в силу свойства 2 решений однородной системы. Мы доказали замкнутость операций в М. Отсюда вытекает, что М – подпространство линейного пространства P⁽ⁿ⁾.

Теорема доказана.

Замечание 1. Легко видеть, что М=P⁽ⁿ⁾ тогда и только тогда, когда А – нулевая матрица.