Главная | Обратная связь

Линейные отображения линейных пространств

Определение 1. Отображение j линейного пространства L в линейное простанство L` называется линейным отображением, если для любых a, bÎL j(a+b)=j(a)+j(b) и "aÎP и "аÎL j(aa)=aj(a).

Лемма 1. Пусть j: L®L` – линейное отображение конечномерного линейного пространства L в линейное пространство L`. Тогда образ любого вектора из L при отображении j однозначно определяется образами векторов некоторого базиса e₁,…,e_n (1) пространства L при этом отображении.

Доказательство. Пусть aÎL. Тогда a=a₁е₁+…+a_nе_n (2). Из определения линейного отображения j имеем: j(a)=j(a₁e₁)+…+j(a_ne_n)=a₁j(e₁)+…+a_nj(e_n) (3). Из (3) видно, что если известны векторы j(e₁),…,j(e_n), то однозначно находится j(a) (ибо координаты вектора а в базисе (1) единственны).

Лемма доказана.

Следствие. Если два линейных отображения j и y n-мерного линейного пространства L в L` над Р совпадают на некотором базисе (1) линейного пространства L, то j=y.

Доказательство. Пусть j и y – линейные отображения L®L`, удовлетворяющие условию: j(e_i)=y(e_i) (i=1,2,..,n). Тогда в силу леммы 1 для любого аÎL имеем: j(а)=y(а), откуда j=y (по определению равенства отображений).

Следствие доказано.

Лемма 2.Пусть L – n-мерное линейное пространство с базисом (1); L<sup>`</sup> – любое линейное пространство над тем же полем Р и c<sub>1</sub>,…, c<sub>n</sub> – произвольные векторы, принадлежащие L`. Тогда существует линейное отображение j: L®L` такое, что j(e_i)=с_i (4) для любого i=1,2..,n, причем такое отображение единственно.

Доказательство. Единственность вытекает из следствия леммы 1.

Докажем существование такого отображения. Так как (1) - базис, то для каждого 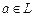справедливо равенство (2) при некоторых α_i Î P. По определению полагаем: , т.е. в (2) все e_i заменили на c_i. Отметим, что j( )ÎL` и j однозначно определяется вектором , т.е. j – отображение L®L`. Докажем линейность j.

Если gÎP, то вектор , и по определению j имеем: .

Далее, если 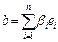, то 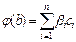. Так как 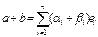,то по определению отображения j имеем: . Таким образом, j(a+b)=j(a)+j(b) "a, bÎL. Следовательно j – линейное отображение.

Осталось проверить справедливость равенства (4).

Так как e_i=0e₁+…+1×e_i+…+0e_n, то по определению отображения j: j(e_i)=0c₁+…+1×c_i+…+0c_n=c_i, т.е. j – искомое отображение.

Лемма доказана.

Замечание 1.Из леммы 2 видно, что для задания линейного отображения n-мерного линейного пространства L в L` достаточно задать n векторов из L`.