Главная | Обратная связь

Барометрическая формула

В равновесном состоянии давление и температура газа одинаковы во всем объеме только в том случае, когда на молекулы не действуют внешние силы. При наличии внешних сил молекулярное движение приводит к своеобразному поведению газов.

Рассмотрим газ, находящийся под действием силы тяжести. Атмосфера (воздушная оболочка Земли) обязана своим существованием наличию одновременно и теплового движения молекул, и силы притяжения к Земле.

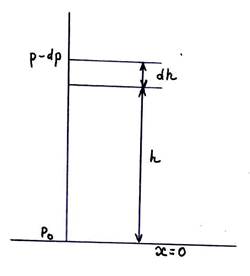
Найдем закон изменения давления газа с высотой. Пусть у поверхности Земли, где высота h = 0, давление Р_О, а на высоте h давление равно Р. При изменении высоты на dh давление изменяется на dp. Величина dР равна разности весов столбов воздуха над площадью, равной единице, на высотах h и h+dh, т.е. равно весу столба воздуха высотой dh с площадью основания в одну единицу:

, где – плотность воздуха, – модуль ускорения свободного падения.

Но 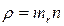, где m_r – масса молекулы, а n – концентрация молекул. Из кинетической теории: ( ), имеем: . После разделения переменных: . Если считать, что то после интегрирования:

где C = const. .

Постоянная С определяется из условия, что при h = 0давление Р = Р_О.

Зависимость давления воздуха от высоты над поверхностью Земли имеет вид:

.

Учитывая, что получаем:

– барометрическая формула.

Давление газа убывает с высотой по экспоненциальному закону. Поскольку давление пропорционально числу молекул в единице объема – концентрации n , то:

Здесь h – разность высот, на которых концентрация молекул n и n_О.

При выводе барометрической формулы предполагалось, что ускорение силы тяжести g = const. Однако это справедливо для небольших h. Из закона всемирного тяготения следует:

, где М – масса Земли, R – радиус Земли. После подстановки g(h) в одну из предыдущих формул:

.

После интегрирования:

, где С = const.

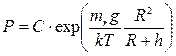; из условия, что при h = 0, Р = Р_О: После подстановки: .

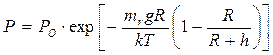Отсюда следует парадоксальный вывод: . Но это невозможно. Следовательно – атмосфера Земли не находится в равновесном состоянии.

 

Закон Больцмана

Барометрическая формула относится к случаю, когда газ находится под действием силы тяжести:

.

Величина есть потенциальная энергия молекулы на высоте h. Поэтому можно сказать, что формула позволяет нам определить число частиц n, энергия которых 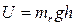, если число частиц с энергией, равной нулю, равно n_о. Если газ находится в каком-либо силовом поле, так что его частицы обладают некоторой потенциальной энергией, то число частиц, обладающих заданной энергией U, определяется формулой:

– формула Больцмана.

Отсюда следует, что – доля частиц, которые в условиях теплового равновесия обладают энергией U.

 

Опыт Перрена

Барометрическая формула была использована Перреном для определения постоянной Больцмана, и, следовательно, числа Авогадро. Перрен предположил, что броуновские частицы, взвешенные в жидкости и подверженные действию силы тяжести, будут распределяться по высоте также, как и молекулы газа.

Эмульсия – две несмешивающиеся жидкости, из которых одна образует меньшие капли, взвешенные в другой. Эти мелкие капли имеют приблизительно сферическую (шарообразную) форму одинакового размера. Микроскоп фокусировался на разные по высоте слои эмульсии. Число частиц в поле зрения позволяло судить о концентрации частиц. Измерения показали, что концентрация частиц действительно убывает с высотой по экспоненциальному закону согласно барометрической формуле, в которой также учтена потеря веса частицы по закону Архимеда.

С учетом силы Архимеда вес частицы: 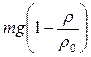, где – плотность вещества частицы; – плотность жидкости, m – масса частицы. Тогда: .

Для двух слоев: .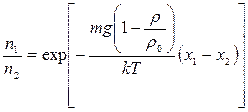

Для определения плотности частицы нужно знать массу и размеры частицы. Радиус частиц эмульсии Перрен определял, измеряя модуль постоянной скорости падения их в эмульсии, заполняющей капиллярную трубку:

– модуль силы сопротивления, определяемой по закону Стокса ( 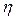– коэффициент вязкости);

– модуль силы Архимеда;

– модуль силы тяжести.

Частица движется с постоянной скоростью при условии, что сумма всех сил, действующих на частицу равна нулю. Или: , откуда радиус частицы:

Плотность частиц равна плотности эмульсии, который определяется по формуле:

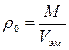, где М – масса эмульсии, V_эм. – объем эмульсии. Отсюда масса частицы

Из формулы 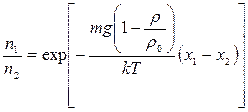, можно определить постоянную

Больцмана: . Поскольку постоянная Больцмана k связана с универсальной газовой постоянной R и числом Авогадро N_А: , то число Авогадро определяется по формуле:

.

Измерив необходимые параметры, входящие в правую часть формулы, в результате расчетов было получено:

 

Основные понятия теории вероятностей

Закон Больцмана, как и барометрическую формулу удобно трактовать, пользуясь понятием вероятности.

Вероятностью события называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при беспредельном увеличении последнего:

Если W₁, W₂, W₃и т.д. – вероятности нескольких исключающих друг друга событий, то вероятность того, что осуществится какое-нибудь одно из них, равно сумме вероятностей всех этих событий.

Вероятность можно определить как отношение числа случаев, благоприятствующих его наступлению, к общему числу возможных случаев, если все случаи равнозначны.

Возвращаясь к формуле Больцмана: величина имеет смысл вероятности. В ней n₀ – общее число возможных случаев, n – число благоприятствующих случаев. Поэтому – вероятность того, что любая из n₀ молекул обладает энергией U.

Вероятность совмещения двух или нескольких независимых событий равна произведению вероятностей каждого из них в отдельности.

Пусть выполнено всего N наблюдений. N₁ – число наблюдений, при которых интересующая величина имеет значение a₁; N₂ – a₂ и т.д. Тогда среднее значение величины:

где N – полное число наблюдений.

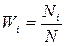– вероятность того, что результат измерения величины а принимает значение а_i.

Средние значение величина а равно сумме произведений отдельных ее значений на соответствующие вероятности:

.

Изучая распределение частиц по скоростям, мы будем искать число частиц, скорости которых лежат в определенном интервале скоростей. Очевидно, что число частиц в единице объема, скорости которых лежат в некотором интервале от до , тем больше, чем больше интервал: или , где а – коэффициент пропорциональности. Величина должна зависеть от скорости, т.е. ; пропорциональна концентрации . В итоге . В пределе: 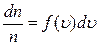. Величину называют функцией распределения – . Величина имеет смысл вероятности: это вероятность того, что любая из молекул газа, лежащих в единице его объема, обладает скоростью, лежащей в интервале вблизи скорости . Величина – вероятность того, что выбранная молекула газа в единице его объема имеет скорость, заключенную в единичном интервале вблизи скорости , поэтому также есть плотность вероятности.