 |
|
Распределение молекул по скоростям (распределение Максвелла)
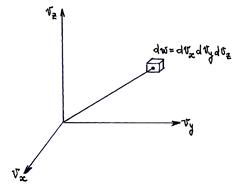 Очевидно, что распределение молекул по различным компонентам скоростей выглядит одинаково:
Очевидно, что распределение молекул по различным компонентам скоростей выглядит одинаково: 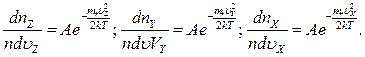
Найдем вероятность того, что компоненты скоростей находятся в интервалах от 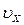 до
до 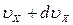 , от
, от 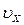 до
до 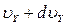 , от
, от  до
до  . Поскольку значение составляющих скоростей независимы, то:
. Поскольку значение составляющих скоростей независимы, то:
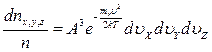
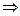
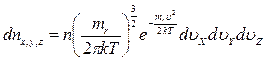
Число молекул в единице объема параллелепипеда:
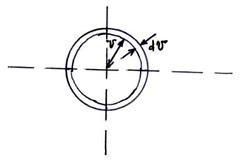
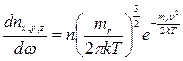
Эта величина не зависит от направления скорости 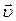 . Шаровой слой в пространстве скоростей состоит из рассматриваемых параллелепипедов.
. Шаровой слой в пространстве скоростей состоит из рассматриваемых параллелепипедов.

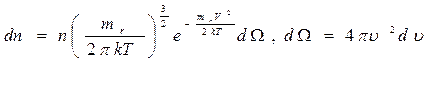
Отсюда:
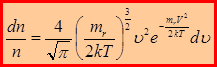 – закон Максвелла распределения молекул по скоростям.
– закон Максвелла распределения молекул по скоростям.
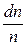 – вероятность того, что у произвольно выбранной молекулы газа модуль скорости окажется в интервале между
– вероятность того, что у произвольно выбранной молекулы газа модуль скорости окажется в интервале между  и
и 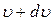 ; это доля всех молекул, скорости которых лежат в интервале от
; это доля всех молекул, скорости которых лежат в интервале от  до
до 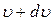 .
.
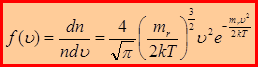 – функция распределения молекул по скоростям.
– функция распределения молекул по скоростям.
а) СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ СКОРОСТЬ.
Число молекул в единице объема, скорости которых заключены в интервале  до
до 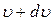 равно
равно 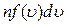 . Сумма скоростей всех таких молекул равна
. Сумма скоростей всех таких молекул равна 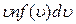 . Сумма скоростей всех молекул, обладающих любыми скоростями:
. Сумма скоростей всех молекул, обладающих любыми скоростями: 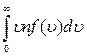 .
.
Средняя арифметическая скорость равна:
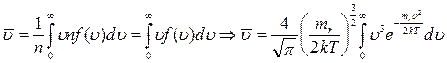
Преобразуем подынтегральное выражение:
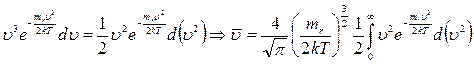
Введем новую переменную: 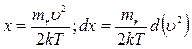 . Тогда:
. Тогда:
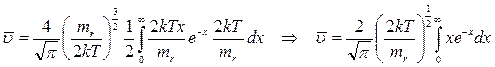
Вычисляем интеграл по частям:
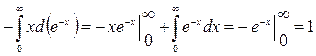 .
.
Следовательно:
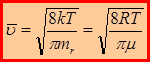 – средняя арифметическая скорость.
– средняя арифметическая скорость.
Можно также показать, что: 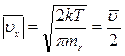
б) СРЕДНЯЯ КВАДРАТИЧНАЯ СКОРОСТЬ
Аналогично предыдущему получаем:
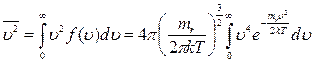 .
.
Записанный интеграл вычисляется аналитически. В результате: 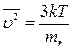
Средняя квадратичная скорость: 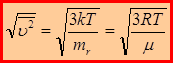 .
.
в) НАИВЕРОЯТНЕЙШАЯ (НАИБОЛЕЕ ВЕРОЯТНАЯ) СКОРОСТЬ
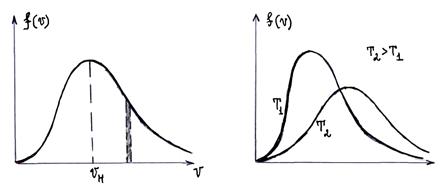
Наивероятнейшая скорость 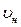 – скорость, около которой группируются скорости наибольшего числа молекул газа. Этой скорости соответствует максимум кривой распределения Максвелла, поэтому она может быть определена на основе исследования на максимум функции распределения
– скорость, около которой группируются скорости наибольшего числа молекул газа. Этой скорости соответствует максимум кривой распределения Максвелла, поэтому она может быть определена на основе исследования на максимум функции распределения 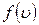 :
:
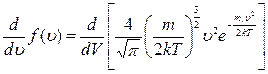
С точностью до const: 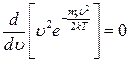
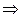
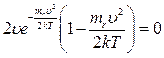 .
.
Уравнение имеет три решения:
1. 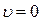 не соответствуют максимуму кривой;
не соответствуют максимуму кривой;
2. 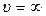 не соответствуют максимуму кривой;
не соответствуют максимуму кривой;
3. 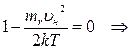
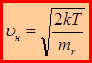 – наивероятнейшая скорость.
– наивероятнейшая скорость.