Главная | Обратная связь

А.ТРА УЕ..А. . САНКТ-ПЕТЕРБУРГ НА ..Е НЕ.Е.. . ПАР...: БУРГУН...

Далее подбираем некоторые слова по смыслу. Весьма вероятно, что.А.ТРА - это ЗАВТРА, ПАР...- это ПАРОЛЬ. С учётом этих предположений сообщение примет вид:

ЗАВТРА УЕЗ.А. В САНКТ-ПЕТЕРБУРГ НА .ВЕ НЕ.ЕЛ. . ПАРОЛЬ: БУРГУН... .

Затем по смыслу окончательно получаем искомое сообщение.

Гг

Задача 1.

.Перед записью в память сервера пароли пользователей системы

преобразуются. Сначала обрабатывается

1-я и 2-я буква пароля, затем 2-я и 3-я и т.д.

Пара букв представляется набором, состоящим

из двенадцати битов x₁,…,x₁₂ , первые шесть

из которых соответствуют первой букве, а вторые

шесть – второй согласно табл.1. Биты получившегося

набора подаются на четыре одинаковых логических

элемента (рис.3). На вход каждого их них поступает три

бита, а на выходе формируется значение f(x,y,z) равное

1, если среди битов x, y, z больше единиц, чем нулей,

иначе формируется значение 0. В память сервера для

каждой пары букв записывают четыре бита:

( f(x₁, x₂, x₃), f(x₄, x₅, x₆), f(x₇, 1 – x₈, x₉), f(x₁₀,1 -x₁₁, x₁₂)).

Определите осмысленный пароль, если в памяти компьютера он хранится в следующем

сжатом виде: (0,1,1,0), (0,0,1,0), (1,0,1,0), (0,0,1,0), (0,0,1,0), (0,0,1,1), (0,0,0,0), (0,1,1,0), (0,0,0,1).

Решение

Задача 2.Каждое из чисел x₁, x₂, x₃, x₄, x₅, x₆ принимает значение либо 0, либо 1.

Известно, что числа x₁ x₂ + x₂x₃ + x₁ x₄, x₁ x₂ x₄ + x₅ x₆ + x₄, x₁ x₂ x₄ + x₄ x₆ + x₂ x₃ ,

x₂ x₆ + x₄ + x₅, x₁ x₄ + x₂x₆ + x₃ чётны, а число x₁ x₄ + x₄x₆ + x₄– нечётно. Найдите

все варианты для x₁, x₂, x₃, x₄, x₅, x₆ .

Решение

Задача 3.В треугольнике ABC известно: BC=2, AC=2, угол ACB равен π/3. Точки M и K

удовлетворяют условиям: AM : MC = 1:2, BK : CK = 2:3. Найдите максимально

возможное расстояние между точками M и K.

Решение

Поместим точку C в начало декартовой системы координат, а точку B на ось абсцисс, как показано на рисунке. Тогда точки C, B, A будут иметь координаты C(0,0), B(2,0), A(3/2,(3√3)/2). Геометрическое место точек K(x, y) таких, что BK : CK = 2 : 3 представляет собой окружность. Действительно,

что эквивалентно

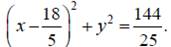
Аналогично, геометрическое место точек M таких, что AM : MC = 1 : 2 - окружность, заданная уравнением

Чтобы расстояние между точками K (лежащей на окружности (1)) и M (на окружности (2)) было максимально, эти точки следует расположить на прямой, проходящей через центры окружностей. Таким образом, искомое максимальное расстояние равно расстоянию между центрами окружностей (1), (2) плюс длины их радиусов:

Задача 4.Милла и Стелла разговаривают по телефону и хотят выбрать секретное число

так, чтобы оно осталось неизвестным постороннему, возможно подслушивающему

разговор. Для этого Милла подбирает натуральное число a ≤ 256 такое, что числа

r₂₅₇( aⁱ ) – различны при всех 1 ≤ i ≤ 256 и r₂₅₇( a²⁵⁶ ) = 1, где r₂₅₇( t ) – остаток от де-

ления числа t на 257. Затем Милла загадывает натуральное число x ≤ 256 , а Стелла–

натуральное число y ≤ 256. После этого Милла сообщает числа a и r₂₅₇(a^x ) Стелле, а

Стелла ей – число r₂₅₇( a^y ). Теперь они обе вычисляют их секретное число r₂₅₇( a^xy ).

Найдите его, если известно, что r₂₅₇(a^x ) = 9, r₂₅₇( a^y ) = 256.

Решение

Обозначим через r₂₅₇( x ) – остаток от деления на 257 числа x.

Так как r₂₅₇(a^x) = 9 = r₂₅₇( 3² ) =r₂₅₇(((r₂₅₇(a^t))²)= r₂₅₇(a^2t ),

де 1 ≤ t ≤ 256, r₂₅₇(a^t ) = 3. Тогда x = 2t или x = 2t - 256 = 2t’.

Тогда r₂₅₇( a^xy ) = r₂₅₇((256)^x ) = r₂₅₇(r₂₅₇((-1)^x ) ) = r₂₅₇((-1)^2t) = 1.

Задача 5.Когда число городов в Криптоландии достигло 4⁴, власти решили провести терри-

ториальную реформу, создав 4 провинции по 3⁴ городов в каждой. В качестве

названий городам планировалось присвоить различные обозначения (a₁, …, a₄) –

наборы из 4-х целых чисел, в которых a_i принимают значения от 0 до 3. При этом

обозначения каждой пары городов из одной провинции должны были отличаться не

нее чем в двух позициях. Укажите какой-либо способ построения такой системы

названий.

Решение

Если число городов m^k, а число провинций m и в каждой по m^k-1

городов, то отнесем к каждой провинции с номером i города с названиями

(a₀, …, a_k-1), удовлетворяющими условиям: сумма a₀₊ …+ a_k-1 кратна i.

Очевидно, что каждый город будет отнесен к какой-либо провинции,и

любые два города в одной провинции будут отличаться не менее чем в 2-х

символах.

Задача 6. Крокодил Гена посылает Чебурашке по радиоканалу сообщение, заменяя его

буквы наборами из нулей и единиц согласно табл.1 (другие буквы не встретились).

Из-за помех некоторые биты исказились, но не более двух в одном наборе.

Определите, какое сообщение отправил крокодил Гена, если Чебурашка получил:

Решение

По условию задачи в каждом наборе искажено не более двух бит. Заметим, что наборы из табл. 1, соответствующие различным буквам, отличаются по крайней мере в трех позициях. Отсюда следует, что искажение одного или двух битов в любом наборе из табл. 1, не делает его другим набором из табл. 1 (на это потребовалось бы по крайней мере три искажения). Значит все те наборы из письма Гены, которые соответствуют наборам из табл. 1, просто не были искажены. Выпишем, соответствующие им буквы: УД*Р*А*Т*Р**Т*И*Т*С*Ч*Д*У*ИХ*Д*Р**

(“*” отмечены пока не известные буквы). Итак, уже имеется некоторая основа сообщения, которая поможет нам подобрать остальные буквы. Для восстановления третьей буквы требуется посмотреть, какие наборы из табл. 1 могли при искажении одного/двух битов стать набором (0,0,1,0,0,0,0), и выбрать тот набор, которому соответствует буква, подходящая по смыслу. Так, набор (0,0,1,0,0,0,0) мог быть получен из набора (0,0,0,0,0,0,0) (при искажении третьего бита) или из набора (1,0,1,0,0,1,0) (при искажении первого и седьмого битов) или из набора (0,0,1,1,0,0,1) (при искажении четвертого и седьмого битов). Очевидно, что по смыслу подходит только набор (0,0,0,0,0,0,0), соответствующий букве А. Аналогичным образом восстанавливаются остальные неизвестные буквы. В результате, получаем письмо Гены.

Задача 7.Для шифрования SMS-сообщений использовался следующий способ. Перво-

начально каждый пробел в исходном сообщении заменялся некоторым трёх-

буквенным словом. Затем полученная цепочка букв набиралась на клавиатуре с

использованием интеллектуального ввода (по типу T9). При этом при вводе

каждой буквы осуществлялась лишь однократное нажатие

соответствующей клавиши (рис.2), а программа интеллектуального

вода выбирала слово из словаря по следующему принципу:

1-я буква слова выбиралась с 1-й нажатой клавиши, 2-я

– со второй и т.д. Полученные таким образом осмысленные слова

разделялись запятыми и передавались. Найдите исходное

сообщение, соответствующее написанному на экране (рис.2).

Решение

Составим таблицу, в которой каждый столбец сформирован из букв,

находящихся на той же клавише, что и исходная:

 

 

Серым цветом выделены те тройки столбцов, которые, по всей видимости,

отвечают вставленному пробелу. Так как символ пробела в тексте встреча-

ется чаще любой триграммы, то из приведенной таблицы можно сделать

вывод, что знак пробела содержится именно в столбцах PАИ (нетрудно из

букв этих столбцов составить слово, например, PАЙ). Двух в подряд идущих

пробелов быть не может. Предположение о том, что столбцы 2,3,4 не обра-

зуют пробел оказывается верным (это случайное совпадение), при этом

зигзагообразно читаем:

Задача 8.Для шифрования передаваемых сообщений Катя и Юра используют следующий способ. Юра заранее выбрал набор коэффициентов (2, 5, 8, 16), натуральное число u и сообщил их Кате. Для шифрования сообщения (x₁,x₂,x₃,x₄), состоящего из нулей и единиц, Катя вычисляет сумму S = 2x₁ + +5x₂+ 8x₃ + 16x₄, а затем находит остаток S′ от деления произведения Su на 32 и отсылает S′ Юре. Помогите Юре расшифровать сообщение S′ = 11, то есть найти соответствующую ему строку (x+++₁,x₂,x₃,x₄) , если известно, что остаток от деления числа 7u на 32 равен 1.

Решение

Обозначим через r_M(b) - остаток от деления числа b на M. Запишем чему равно число S′ согласно определению деления натуральных чисел с остатком:

Поскольку известно, что остаток от деления 7u на M равен 1, то запишем:

Домножим обе части (1) на 7 и подставим в полученное равенство вместо 7u равенство (2). Имеем:

Заметим далее, что натуральное число

Поэтому полученное равенство (3) есть не что иное, как деление 7S′ с остатком на M и, кроме того, r_M( 7S′) = S. Таким образом, найдя остаток от деления 7S′ на M , получим исходное число S.

В нашем случае, Теперь, зная S, осталось найти (x₁,x₂,x₃,x₄). Но это делается легко. Действительно, равенство x₄ = 0 очевидно, поскольку S < 16. Дальше можно перебрать все возможные восемь вариантов, либо сразу заметить, что x₂ = x₃ = 1, x₁ = 0(что просто угадывается), либо последовательно вычитать из S числа a₃,a₂, a₁ пока не получим нуль, полагая при этом, что соответствующий x_i = 1.

Задача 9.Для шифрования сообщения использовалось устройство из трёх последовательно зацепленных шестерёнок с 5, 30 и 6 зубцами (рис.1). На зубцах первой шестерёнки записаны цифры от 1 до 5, а на третьей – от 1 до 6. На второй шестерёнке также по часовой стрелке записан тридцатибуквенный алфавит: АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЫЬЭЮЯ. Для каждой шестерёнки выделено окошко (на рис.1 оно изображено квадратиком), в котором видна лишь одна буква или цифра. Сообщение шифровалось побуквенно: вторая шестерёнка вращалась по часовой стрелке, пока в окошке не появится первая буква сообщения. Затем выписывалась пара цифр, открывшихся в окошках первой и третьей шестерёнок. Далее продолжали вращать вторую шестерёнку до появления второй буквы сообщения, выписывали пару цифр из окошек и т. д. Так для случая, приведенного на рис.1, буква Б заменяется парой 52 (подчеркнем, что рисунок лишь поясняет принцип работы устройства, и на самом деле букве Б может соответствовать другая пара цифр). Начальное взаимное расположение шестерёнок неизвестно. Найдите по известным выписанным парам цифр 11 55 16 53 21 16 31 15 52 14 16 44 46 какое сообщение было зашифровано (пробелы в тексте сохранены).

Решение

Заметим, что если вторая (центральная) шестеренка повернута на x позиций по часовой стрелке относительно начального положения, то буква в окошке меняется на букву, отстоящую от нее на x позиций, но против часовой стрелки.

, то появившиеся в окошках цифры однозначно определяют величину x´= При этом шестеренки с цифрами будут повернуты против часовой стрелки и так как 3056

сдвига относительно начального положения, которым можно считать положение, при котором на цифровых шестеренках выставлены две единицы (см. таблицу).

Рассмотрим теперь текст: 11 55 16 53 21 16 31 15 52 14 16 44 46 Заменим пары цифр на величины поворотов:

Предположим что первое слово – это предлог У. Тогда найдём числовые величины поворота второго колеса, соответствующие всем буквам.

Заменим величины поворотов на буквы, получим ответ.

Гг

Задача 1.Пусть – число, стоящее в строке с номером i и столбце с номером j квадратной таблицы А (табл. 6). По таблице А построена таблица В, в строке с номером i и столбце с номером j которой стоит выражение . Набор из десяти клеток таблицы будем называть «правильным», если в нем присутствуют ровно по одной клетке из каждого столбца и каждой строки. Вычисляются произведения элементов, входящих в правильные наборы. Результатом являются выражения вида 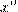. Найдите наибольшую возможную степень правильного набора (число n) и число правильных наборов степени 1023.

Решение

Наибольшая возможная степень правильного набора получается при перемножении элементов, стоящих в таблице B на местах, соответствующих местам в таблице A, которые в табл. 6 выделены жирным шрифтом. Поэтому наибольшая степень равна .

Табл. 6

Чтобы решить вторую часть задачи, заметим, что верно следующее:

Отсюда следует, что искомый коэффициент равен числу таких наборов по 10 элементов, стоящих в различных строках и столбцах в табл. 6, в которых каждое число от 0 до 9 встречается по одному разу. Любой такой набор распадается на 3 набора: набор с числами 2, 3, 4 в нижнем правом квадрате, набор с числами 0, 1, 9 в центральном квадрате и набор с числами 5, 6, 7, 8 в верхнем левом квадрате. Непосредственной проверкой убеждаемся в том, что в каждом из указанных квадратов соответственно имеется 3, 3 и 8 таких наборов, следовательно, общее число наборов равно 3*3*8 = 72.

Задача 2.В картинке, вышитой «крестиком», Ксюша скрыла послание Сереже (см. рис. 3). Буквы она заменила парами цифр в соответствии с алфавитным порядком: А=01, Б=02, …, Я=33. Затем Ксюша выбрала простое число р. Для цифры послания с номером k крестик нужного цвета вышивался в клетке с номером рk. Нужный цвет определялся по рис. 4, а клетки в схеме нумеруются слева направо снизу вверх (например, левая нижняя клетка имеет номер 1, а клетка над ней - 51). Затем Ксюша завершила оставшуюся часть картинки. Прочитайте скрытое послание.

Решение

Так как буквы русского алфавита представлены их номе-

Рис. 3

х . & : * > < s = ж Рис. 4.

рами алфавита, то первый символ послания может быть только «ж», «х», «.» или «&». Рассмотрим позиции с простым номером в первой строке, в которых записаны именно эти символы: 2, 29, 37 и 47. Значит, данные числа могут являться кандидатами на выбранное Ксюшей число p, поскольку на этих местах могут находиться цифры послания с номером . Начинаем выбирать клетки картинки, двигаясь по строкам слева направо снизу вверх с шагом, равным p. Как только на нечетном месте встречается неподходящий символ (т.е. отличный от «ж», «х», «.», «&»), делаем вывод, что p выбрано не верно (см. табл. 5).

 

Табл. 5

Рис. 5

В рис. 5 цветами выделены «цвета» (согласно рис. 4) для значений p, равных 37 и 47.

Задача 3.Номера гостиницы Криптохауз открываются магнитными карточками, на которых записаны ключевые последовательности из нулей и единиц длины 8. Чтобы карточка открыла номер класса «эконом» необходимо, чтобы на ней был записан ключ вида (10****0*), номер «стандарт» - ключ вида (**1*1***), «люкс» - (1****0**). На местах, помеченных символом «*», может быть любой из двух символов. Каждый из 176 работников Криптохауза имеет ровно по 5 различных ключей и может использовать только их. Известно, что любой из существующих ключей изготовлен ровно в 16 экземплярах и находится в пользовании. Найдите минимальное число работников, открывающих номера класса «эконом», если получена информация о наличии ключей существующих типов (см. табл. 1).

Табл.1:

Вид	Количество
(**1*1***)
(1****0**)
(101*1*0*)
(1*1*10**)
(10***00*)
(101*100*)

Решение

Найдем общее число различных ключей. Для этого посчитаем количество всех используемых в гостинице ключей с учетом их повторений. Если x – общее число различных ключей, то количество всех используемых ключей с учетом их повторений равно 16х, поскольку каждый ключ изготовлен ровно в 16 экземплярах. В то же время, каждый из 176 работников имеет ровно по 5 различных ключей, а значит количество используемых в гостинице ключей с учетом их повторений равно 176×5 = 880. Отсюда, 16х=880 и х=55.

Теперь найдем количество ключей, открывающих номера класса «эконом». Ясно, что ключи имеющихся трех видов связаны так называемой диаграммой Эйлера (см. рис. 2). Пометим получившиеся 7 областей соответствующими числами. Так, например, области 7 соответствуют ключи, открывающие номера всех типов, области 1 – только номера класса «эконом» и т.д.

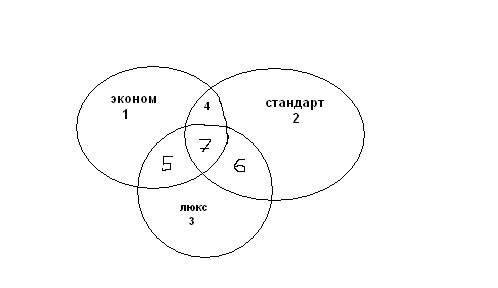
В соответствии с условием задачи, составим таблицу количества ключей, находящихся в различных областях диаграммы (табл. 2).

Табл. 2
Область	4U7U6U2	5U7U6U3	4U7	6U7	5U7
Количество

 

Из полученной таблицы легко найти количество ключей в каждой из областей 2,…,7, находя последовательно число элементов сначала в областях 4,5,6, а затем в 2,3. Эти данные запишем в таблицу (табл. 3).

Табл. 3
Область
Количество

Чтобы найти количество ключей, открывающих номера класса «эконом», нужно найти количество ключей, находящихся в области 1U4U5U7. Для этого вычтем из общего числа различных ключей суммарное количество ключей, находящихся в других областях: 55 – (7+9+15) = 24. Итак, количество ключей, открывающих только номера класса «эконом» равно 24.

Найдем минимальное число работников, имеющих ключи, которые открывают номера класса «эконом». Покажем, что это число равно [16·24/5]=77, где [x] – наименьшее целое, больше либо равное x. Расположим данные ключи в табл. 4 размера 16 на 24, в столбцах которой будут экземпляры одного и того же ключа, и покроем ее элементы «пятерками» - наборами, содержащими не более 5 различных ключей.

Табл. 4

В этих терминах задача переформулируется так: найти минимальное число «пятерок», покрывающих построенную таблицу. Начнем покрывать ее с первой строки. Ясно, что минимальное число «пятерок» равно 4, т.к. 24=5·4+4, значит оставшееся число ключей в первой строке равно 4. Теперь выберем во второй строке один отличный от этих 4-х ключей ключ (они образуют «пятерку»), и покроем строку минимальным числом «пятерок» (их ровно четыре), тогда оставшееся число ключей во второй строке равно 3. Продолжим данный процесс, выбирая в очередной строке подходящее число ключей для образования «пятерки» с оставшимися ключами предыдущей строки, и разбивая затем строку на минимальное число «пятерок».

Как видно, набор остатков в каждых последовательно идущих пяти строках будет одинаковым. Всего таких повторений - 3, т.к. 16=5·3+1, а каждое такое повторение строк дает 5·4+4=24 «пятерок». Итого всего «пятерок», приходящихся на 15 строк, будет 24·3=72. Таким образом, остается одна строка (последняя), которая даст 4 «пятерки», и в остатке еще 4 ключа, которые покроет еще одна «пятерка». Отсюда, общее их количество равно 72+4+1=77.

Задача 4.Докажите, что из любых пяти различных натуральных чисел всегда можно выбрать три различных числа так, что их сумма будет делиться на три. Докажите, что из любых двадцати пяти различных натуральных чисел всегда можно выбрать девять различных чисел так, что их сумма будет делиться на девять.

Решение

Решим сначала первую часть задачи. Пусть - различные пять натуральных чисел и - их остатки от деления на 3 соответственно. Возможны следующие два случая: а) среди чисел есть хотя бы три одинаковых, тогда сумма этих трех чисел делится на три; б) среди чисел нет трех одинаковых, а значит, найдутся три различных числа, имеющие остатки 0, 1 и 2 и тогда их сумма делится на три. Докажем теперь второе утверждение задачи. Пусть - любые двадцать пять натуральных чисел. Будем считать, что они упорядочены по возрастанию. Сгруппируем их последовательно по 5 штук:

В каждой пятерке по первой части задачи найдется три различных числа, сумма которых делится на три, выпишем их:

Рассмотрим пять различных натуральных чисел: Среди этих пяти чисел по доказанной первой части задачи найдутся три различных числа, пусть a, b, c, сумма которых делится на три. Каждое из чисел a, b, c есть от суммы трех некоторых различных чисел из набора тогда a + b + c есть от суммы некоторых девяти различных чисел из этого же набора. Отсюда из свойств делимости целых чисел следует, что сумма этих девяти чисел делится на 9.

Задача 5.При установке TCP/IP соединения между компьютерами А и В используется так называемая «процедура рукопожатия»: 1) А выбирает натуральное число х, не большее 5988, и передает В значение функции F(x), а В отвечает А числом F(x+1); 2) В выбирает натуральное число у, не большее 5988, и передает А число F(y), при этом А отвечает В числом F(y+1). Значение функции F равно остатку от деления на 5989 значения аргумента, возведенного в третью степень. Найдите х и у, если в сети последовательно наблюдались числа: 1369,1421, 2795 и 2804. Число 5989 выбрано так, что значение аргумента определяется по значению функции F однозначно.

Решение

Исходя из условия задачи, составим систему уравнений в общем виде для , где - это либо , либо : - известны. Заметим, что тогда получаем Для первой пары чисел: ; тогда Для второй пары чисел: ; тогда

Задача 6.При раскопках стоянки древних хакеров археологами были обнаружены следующие предметы, вероятно, использовавшиеся для шифрования информации: линейка (см. рис. 1), и катушка с белой нитью, на которую были нанесены черные метки. Расстояния между последовательными метками, измеренные в единицах деления линейки, равны 74.5, 85, 90, 90, 86, 18. Прочитайте сообщение, зашифрованное хакерами.

Рис1.:

Решение

Анализ линейки на рис. 1 позволяет догадаться о способе наматывания нити для осуществления шифрования. Наматывание нити производилось так, что с оборотной стороны линейки нить ложилась вертикально, а с лицевой – диагонально. В этом случае возможны два варианта наматывания нити: от «б» к «з» или наоборот. Перебором двух вариантов устанавливаем, что наматывание нити осуществлялось по вертикали сверху вниз, по диагонали – снизу вверх, а скрытым текстом являлось слово «фишинг».

Задача 7. Для записи текста используются только заглавные буквы, пробелы, точки и запятые – всего различных 36 символов. При зашифровании каждый символ заменили числом от 0 до 35 в соответствии с порядком в «расширенном» алфавите. Затем полученную последовательность чисел разбили на пары, а каждую пару заменили по правилу: пару заменили на пару , где – остаток от деления числа x на 36, а n, k и m – заранее выбранные целые числа от 0 до 35. Найдите все наборы чисел n, k и m, при которых разные пары переходят в разные (это необходимо для возможности расшифрования текста). Сформулируйте правило расшифрования для случая n = k = m = 17. Решение обоснуйте.
Решение

Условие задачи равносильно тому, что при «правильно» выбранных n, k и m система состоящая из уравнений ┤ имеет единственное решение при любой паре 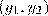. В этом случае разные пары будут переходить в разные 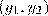, иначе получим противоречие с единственностью решения такой системы при некоторой паре 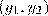. Обратно, если разные пары переходят в разные пары 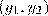, то при любой паре 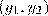такая система либо имеет единственное решение, либо не имеет решений. Однако в то же время количество различных пар равно , а значит количество соответствующих им различных пар 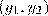по крайней мере , но ясно, что их число не превосходит , а стало быть оно в точности равно . Отсюда следует, что для любой пары 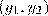рассматриваемая система имеет решение и при том только одно. Можно показать, что уравнение 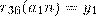имеет единственное решение при любом 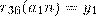тогда и только тогда, когда n и 36 взаимнопросты. Следовательно, если n и 36 взаимнопросты, то из данного уравнения значение находится однозначно и тогда второе уравнение системы примет вид: . Аналогично, оно имеет единственное решение относительно при любом тогда и только тогда, когда m и 36 взаимнопросты, при этом значение параметра k на это свойство никак не влияет. Таким образом, однозначное расшифрование возможно при выборе взаимнопростых с 36 числах n, m и произвольном k. Пусть теперь n=k=m=17. Тогда для нахождения нужно решить систему уравнений: . Легко видеть, что . Отсюда легко проверить, что и .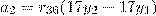

Задача 8.При передаче сообщения по факсу произошел сбой. В результате на листе было напечатано

 

 

Восстановите текст (ответ обоснуйте). Известно, что исходный шрифт выглядел так

АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.

Решение

Сопоставим каждому изображенному символу возможные соответствующие ему буквы алфавита и затем попробуем, выбирая по одной букве из каждого столбца, прочитать исходное сообщение:

В таком случае этот метод сводится к так называемому чтению в колонках, или по-другому, зигзагообразному чтению. Для восстановления исходного сообщения каждой полученной искаженной букве ставится в соответствие набор возможных ее истинных значений в зависимости от искажений , после чего становится возможным применение зигзагообразного чтения для нахождения осмысленного текста.

Задача 9.Известно, что десятизначное число A = 2013x2013y делится нацело на 121. Найдите все возможные пары цифр (x,y). Решение обоснуйте.

Решение

Заметим, что 121=11⋅11. Используя признак делимости на 11 (знакопеременная сумма цифр числа должна делиться на 11) получаем, что число А делится на 11 только при условии x = y. Действительно, знакопеременная сумма цифр числа А

равна: y+1+2+3+0-(3+0+x+1+2)=y-x.

Но y и x являются цифрами, следовательно |y-x|<11, поэтому делимость возможна тогда и только тогда, когда x = y.

Отсюда, число А имеет вид 2013x(10⁵+1). Непосредственной проверкой можно убедиться, что 10⁵+1 делится на 11, но не делится на 121. Следовательно, на 11 должно делиться число 2013x. Используя признак делимости на 11, находим, что x = 0, а значит и y = 0.

Гг

Задача 1.Для хранения пароля, записанного в 32-х буквенном алфавите, каждая его буква представляется порядковым номером -- парой цифр (т.е. А - 01, Б - 02 и т.д.). Получается последовательность цифр . Одновременно по правилу , вырабатывается последовательность десятичных цифр , минимальный период которой равен 10, где -- остаток от деления на 10, -- натуральные числа. После чего по правилу вычисляется последовательность , которая и сохраняется в памяти компьютера. Вася выбрал для пароля очень короткое слово, поэтому при вводе был вынужден повторить его дважды. Помогоите ему восстановить забытый пароль, если сохраненная последовательность имеет вид: 3,4,8,4,3,8,8,2,7,9,2,8,7,2,2,6.

Решение

ПОскольку длина получившейся последовательности равна 16 и введенное слово повторялось дважды, то последовательность является периодической с периодом 8. Имеем соотношения:

. Тогда

.

Поэтому,

Имеем: .

Получим уравнение: . Данному уравнению удовлетворяют два значения: или a = 6. Но так как период равен 10, то нетрудно проверить, что правильным вариантом является a = 1. Тогда

.

Отсюда b = 3 или b = 8. Аналогично, исходя из периода 10, истинным вариантом будеи только b = 3. Таким образом, получаем

.

Теперь для нахождения ключевого слова достаточно перебрать 4 вырианта для . При каждом фиксированном , зная , вычисляем , после чего восстанавливаем всю последовательность в соответствие с полученным законом рекурсии. Зная , находим все остальные значения .

Единственный читаемый вариант ключевого слова соответствует слову <<ЯШМА>>

Задача 2.На соревнованиях беговых роботов было представлено некоторое количество механизмов. Роботов выпускали на одну и ту же дистанцию попарно. В протоколе фиксировались разности времен финиша победителя и побежденного в каждом из забегов. Все они оказались разными: 1 сек., 2 сек., 3 сек., 4 сек., 5 сек., 6 сек. Известно, что в ходе бегов каждый робот соревновался с каждым ровно один раз, и что каждый робот всегда бегал с одной и той же скоростью. Определите число представленных на бегах механизмов, а также время прохождения дистанции каждым из них, если лучшее время прохождения дистанции было равно 30 секундам.

Решение

Пусть в забеге участвовало роботов. Из условия задачи следует, что количество "попарных" забегов (т.е. каждый с каждым) равно 6. Это число равно

поскольку первый робот должен пробежать с другими роботами, второй уже с другими и т.д. Имеем квадратное уравнение:

из которого находим, что его единственное натуральное решение

Обозначим через 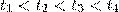-- временные результаты забегов 4-х роботов в порядке их строгого возрастания . Ясно, что самый медленный робот с результатом отстал от самого быстрого ( ) на 6 секунд и поэтому его результат -- секунд. Остается найти .

Поскольку в одном из забегов имеется разность 5 секунд, то перебирая все возхможные случаи и используя тот факт, что разности времен забегов -- целые числа, придем к двум возможным вариантам:

, откуда ;

, откуда .

В обоих вышеперечисленных случаях результат забега оставшегося робота определяется однозначно: 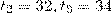соответственно, в силу того, что разности времен забегов различны.

Задача 3.В таблицу, состоящую из строк и столбцов, записаны числа так, что сумма элементов в каждой строке равна 790, а сумма элементов в каждом столбце равна 1422. Найдите числа и , при которых выражение принимает наименьшее возможное натуральное значение. При найденных параметрах и приведите пример указанной таблицы, в которой не все элементы одинаковы.

Решение

Сумма всех элементов таблицы равна и в то же время она равна , поэтому:

тогда и только тогда, когда

Отсюда 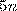кратно 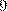и кратно 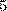, а поскольку НОД(5,9)=1, постольку из свойств делимости вытекает, что .

Наименьшее значение выражения

очевидно, равно при . В таком случае .

Задача 4.Винтик и Шпунтик разработали следующую систему шифрования. Исходный текст, записанный без пробелов, разбивается последовательно на части по 10 букв. В каждой части буквы нумеруются слева направо от 1 до 10 и затем переставляются по правилу, которое задаётся таблицей 1. То есть, первая буква каждой части ставится на 7 место, вторая – на 9 место и т.д. Однажды Винтик собрался отправить сообщение Шпунтику. Он его зашифровал, а потом, для пущей надежности, зашифровал полученный текст еще раз. Подумал, и зашифровал его еще 75 раз. В результате Шпунтик получил вот такое сообщение: «ыновтекнафнтеамошйек» Помогите Шпунтику его прочитать.

Решение

Заметим, что буквы переставляются по правилу

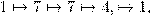
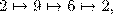
Значит, каждая буква из первой и второй цепочки встанет на свое место после 3-х шифрований, а из третьей цепочки – после 4-х шифрований. Стало быть, все буквы встанут на свое место через шифрований. Таким образом, через каждые 12 шифрований снова будет появляться исходный текст.

Винтик зашифровывал свое сообщение 335 раз. Поделим с остатком 335 на 12:

Значит, если зашифровать текст, который получил Шпунтик еще раз, то получим 336 шифрований, где число 336 кратно 12, и получится исходное сообщение: «УМЕНЯЕСТЬСЕНОКОСИЛКА».

Задача 5.Функции с областью определения и областью значений заданы таблицами (табл.1).

табл. 1

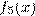
(а) для функции , заданной равенствами подберите различные числа такие, чтобы соотношение

(1)

выполнялось для всех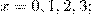

(б) докажите, что для любой функции с областью определения и областью значений , переводящей разные элементы в разные, найдутся числа (не обязательно различные) при которых выполнено равенство (1).

Решение

(б) Пусть . Выберем среди такую функцию , что . Пусть . Ясно, что . Выберем среди функцию такую, что . Тогда функция 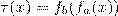удовлетворяет условию . Пусть . Ясно, что . Выберем среди функцию такую, что . Тогда функция 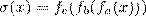удоволетворяет равенствам . Значит, и для всех

(а) Используя рассуждения п.(б) можно прийти к одному из вариантов ответа: a = 2, b = 5, c = 6.

Задача 6. Разблокировка коммуникатора осуществляется вводом 4-значного числового кода на сенсорном экране. На клавиатуре первоначальная расстановка цифр после ввода кода меняется в зависимости от случайного простого числа 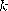от 7 до 2017, и на месте цифры отображается значение равное последней цифре числа . Пользователь вводит цифры из левой колонки левой рукой, а остальные правой. Восстановите код блокировки, если известно, что при наборе кода пользователь вводил цифры следующим образом:

при : левой, правой, правой, правой;

при : правой, правой, левой, левой;

при : левой, левой, правой, правой;

при : правой, правой, левой, правой.

Решение

Из признаков делимости на 2 и на 5 следует, что простое число не может оканчиваться на четную цифру и на цифру 5. Следовательно, такое простое число может оканчиваться лишь на цифры 1, 3, 7, 9. Обозначим, через – последнюю цифру числа , тогда ясно, что выполняется свойство: . Поэтому раскладка клавиатуры определяются лишь указанными последними цифрами – 1, 3, 7, 9. Таким образом, возможны 4 варианта раскладки клавиатуры:

Теперь несложно понять, что в условиях задачи следует рассматривать все раскладки:

Первая цифра кода при находится в первом столбце, значит это 1, 4 или 7, при эта цифра лежит также в первом столбце – следовательно, она равна 7. Вторая цифра кода при лежит в первом столбце, значит это 7, 8 или 9. Во всех остальных раскладках она лежит в других столбцах (2 -ом или 3-ем). Как видно, таким свойством обладает только цифра 8. Аналогичным образом рассуждая, придем к тому, что единственной комбинацией, удовлетворяющей условиям задачи, будет 7832.

Гг

Задача 1.

Задача2.

Решение

Задача 3.

Задача 4.

Задача 5.Докажите, что нельзя обойти все клетки изображенной на рисунке фигуры, побывав в каждой ровно один раз. Начинать движение можно из любой клетки. Разрешается двигаться на одну клетку только вправо, влево, вверх или вниз. Движение по диагонали запрещено.

Решение

Раскрасим клетки как на рисунке. Делая один шаг, мы из черной клетки попадаем в белую и наоборот. Значит, если бы искомый обход был возможен, то клеток одного цвета было бы от силы на единицу больше, чем клеток другого цвета. Но черных клеток на две больше, чем белых. Поэтому обход невозможен.

 

Задача 6.Линия связи состоит из 4-х каналов, пронумерованных числами 1,2,3,4. Для передачи по линии сигнала на каждый канал подается свой импульс,