Главная | Обратная связь

Первое начало термодинамики

Внутренняя энергия U термодинамической системы состоит из кинетической энергии всех внутренних движений частиц (поступательных, вращательных, колебательных) и потенциальной энергии их взаимодействия. Для идеального газа пренебрегают потенциальной энергией. Поэтому внутренняя энергия идеального газа определяется кинетической энергией его молекул, которая зависит только от температуры.

Внутренняя энергия является функцией состояния, т.е. определяется только состоянием системы (в данном случае – температурой) и не зависит от вида перехода в это состояние.

Если система совершает круговой процесс (цикл), возвращаясь в начальное состояние, то полное изменение её внутренней энергии равно нулю: . Как известно, математически это соотношение означает, что элементарное изменение dU является полным (точным) дифференциалом.

Изменить внутреннюю энергию системы можно двумя способами: 1) совершить механическую работу; 2) сообщить системе или отнять у неё некоторое количество теплоты.

Первое начало термодинамики: количество теплоты, сообщённое системе, идет на приращение её внутренней энергии и на совершение системой работы над внешними телами:

DQ = DU + DA или dQ = dU + dA. (40)

Входящие в формулу (40) величины могут быть как положительными, так и отрицательными. Если количество теплоты передается системе, она нагревается и сама совершает работу над внешними телами, то величины – положительны. Если количество теплоты отбирается от системы, она остывает, и внешние силы совершают над ней работу, то величины – отрицательны.

Если система, например рабочее тело, в периодически действующем двигателе совершает круговой процесс (цикл), т.е. возвращается в исходное состояние, то DU = 0 и при этом DA = DQ. Отсюда следует вторая формулировка первого начала термодинамики: невозможен вечный двигатель первого рода, т.е. такое периодически действующее устройство, которое бы совершало работу в большем количестве, чем полученная им извне энергия.

Найдём работу, которую совершает газ при расширении. Пусть газ, действуя на поршень с силой F = pS, перемещает его на расстояние dx (рис. 22) и совершает элементарную работу

dA = F dx = pS dx = p dV.

Полная работа находится интегрированием:

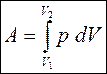. (41)

На графике в координатах (p, V) работа равна площади фигуры, ограниченной осью V, прямыми V₁ и V₂ и кривой p = f (V). Из рис. 23 видно, что работа (площадь под кривой) зависит от вида перехода системы из состояния 1 в состояние 2. Поэтому работа А не является функцией состояния, а её элементарное изменение не является полным дифференциалом. Для элементарной работы употребляют обозначения dА или d¢A (а не дифференциал dA).

Если внешние силы умень­шают объём газа (рис. 24), то при интегрировании получается «отрицательная» работа, так как верхний предел интегрирования V₂ меньше нижнего V₁.

Применим первое начало термодинамики к изопроцессам.

Изохорический процесс V = const (рис. 25). Так как V = const, то dV = 0 и DА = 0. Из уравнения первого начала термодинамики (40) остается DQ = DU. В изохорическом процессе всё количество теплоты, подводимое к системе, полностью идет на изменение её внутренней энергии.

Изобарический процесс р = const (рис. 26). В этом процессе изменяется внутренняя энергия и совершается работа dQ = dU + pdV. Работа в данном случае вычисляется очень просто (это площадь прямоугольника):

. (42)

Выражение (42) определяет физический смысл газовой постоянной: если n = 1 моль и Т₂ – Т₁ = 1 К, то А = R, т.е. газовая постоянная R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К[Дж/(моль×К)].

Изотермический процесс T = const (рис. 27). В этом процессе dU = 0, следовательно, dQ = dA, т.е. всё подводимое количество теплоты тратится на совершение работы. Для нахождения работы выразим зависимость p = f (V) из уравнения Менделеева-Кла­пейрона: p = nRT/V. Работа равна:

. (43)