 |
|
Принцип найменшої дії.
Найбільш загальне формування закону руху механічних систем дається так званим принципом найменшої дії(або принципом Гамільтона). Згідно з цим принципом кожна механічна система характеризується певною функцією
, або в скороченому записі 
, причому рух системи задовольняє такій умові:
Нехай в моменти часу 
і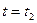 
система певні положення, що характеризуються двома наборами значень координат 
і 
. Тоді між цими положеннями система рухається таким чином, щоб інтеграл
(1)
мав найменше можливе значення.
Функція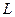 
називається функцією Лагранжа даної системи, а інтеграл (1) – дією.
Для спрощення запису формул спочатку припустимо, що система має всього одну ступінь вільності, так що повинна бути визначена всього одна функція 
.
Нехай 
і є функція, для якої 
має мінімум. Це означає, що зростає при заміні на функцію виду
, (2)
де 
- функція, мала на всьому інтервалі часу від 
до 
(її називають варіацією функції ).
Так як при і 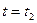всі порівнювані функції (2) повинні набувати одні й ті ж значення і , то повинно бути:
(3)
Зміна при заміні 
на 
дається різницею:
Розклад цієї різниці по степеням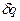 
і 
(в підінтегральному виразі) починається з членів першого порядку. Необхідною умовою мінімальності є перетворення в нуль сукупності цих членів; її називають першою варіацією інтегралу. Отже, принцип найменшої дії можна записати у вигляді:
(4)
або виконавши варіювання
Відмітивши, що 
, про інтегруємо другий член по частинам і отримаємо:
(5)
Але враховуючи умови (3) перший член в цьому виразі зникає. Залишається інтеграл, який повинен дорівнювати нулю при довільних значеннях 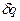. Це можливо тільки в тому випадку, якщо підінтегральний вираз тотожно перетворюється в нуль. Отже, ми отримаємо рівняння
При наявності кількох ступенів вільності в принципі найменшої дії повинні залежно варіюватися різних функцій 
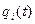. Очевидно, що ми отримуємо тоді рівнянь виду
(і=1,2,..., ) (6)
Це шукані диференціальні рівняння; вони називаються в механіці рівняннями Лагранжа.
Якщо функція Лагранжа, даної механічної системи відома, то рівняння (6) встановлюють зв’язок між прискореннями, швидкостями і координатами, тобто вони є рівняннями руху системи.
Зазначимо, що функція Лагранжа визначена лише з точністю до додавання до неї повної похідної від довільної функції координат і часу.