Главная | Обратная связь

Функція Лагранжа вільної матеріальної точки.

Завжди можна знайти таку систему відліку, по відношенню до якої простір є однорідним і ізотропним, а час – однорідним. Така система називається інерціальною. Ми можемо тепер зробити деякі висновки про вид функції Лагранжа матеріальної точки, що вільно рухається в ІСВ. Однорідність простору і часу означає, що ця функція не може містити явним чином ні радіус-вектора точки, ні часу , тобто 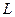є функцією лише від швидкості 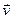. В силу ж ізотропії простору функція Лагранжа не може залежати також і від напряму вектора 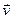, так що є функцією лиши від його абсолютної величини, тобто від квадрату

(1)

Для знаходження виду залежності функції Лагранжа від квадрата вектора швидкості, скористаємося принципом відносності Галілея. Якщо ІСВ рухається відносно ІСВ з нескінченно малою швидкістю , то

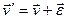
Так як рівняння руху у всіх системах відліку повинні мати один і той же вигляд, то функція Лагранжа повинна при такому перетворенні перейти в функцію , яка, якщо і відрізняється від , то лише на повну похідну від функції координат і часу

Розклавши цей вираз в ряд по степеням і нехтуючи нескінченно малими вищих порядків, отримаємо

Даний член правої частини цієї рівності буду повною похідною по часу тільки в тому випадку, якщо він залежить від швидкості 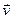лінійно. Тому від швидкості не залежить, тобто функція Лагранжа в даному випадку прямо пропорційна квадрату швидкості:

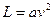
З того, що функція Лагранжа такого виду задовольняє принципу відносності Галілея у випадку скінченної швидкості системи відліку відносно . Дійсно,

Другий член є повною похідною і може бути відкинутий. Постійна а прийнято позначати як , так що врешті напишемо функцію Лагранжа точки, що вільно рухається, у вигляді:

, де - маса матеріальної точки.

Для системи не взаємодіючих точок

Корисно відмітити, що

Тому для складання функції Лагранжа досить знайти квадрат довжини елемента дуги у відповідній системі координат.

В декартових координатах, наприклад, , тому