Главная | Обратная связь

Функція Лагранжа системи матеріальних точок.

 

Розглянемо замкнуту систему матеріальних точок, що взаємодіють між собою. Взаємодію між, матеріальними точками можна описати доповненням до функції Лагранжа не взаємодіючих точок певної(залежно від характеру взаємодії) функції координат.

Позначивши цю функцію через - 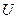, напишемо:

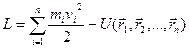(1)

де - радіус n-ї точки.

Суму = називається кінетичною енергією, а функцію 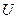- потенціальною енергією системи.

Той факт, що потенціальна енергія залежить тільки від розміщення всіх матеріальних точок в один і той же момент часу, означає, що зміна положення однієї з них миттєво позначається на всіх останніх; можна сказати, що взаємодії „поширюються” миттєво. Це пов’язано з основними передумовами класичної механіки – абсолютністю часу і принципом відносності Галілея. Якби взаємодія розповсюджувалась не миттєво, тобто з кінцевою швидкістю, то ця швидкість була б різною в різних(що рухаються одна відносно іншої) системах відліку, бо абсолютність часу автоматично означає застосовність правила додавання швидкостей до всіх явищ. Але тоді закони руху взаємодіючих тіл були б різними в різних (інерціальних) системах відліку, що суперечило б принципу відносності.

Знаючи функцію Лагранжа, ми можемо скласти рівняння руху

(2)

Підставивши сюди (1), отримаємо:

(3)

Рівняння руху в цій формі називаються рівняннями Ньютона і являють собою основу механіки частинок, що взаємодіють.

Вектор

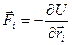(4)

що стоїть в правій стороні рівнянь (3), називається силою, що діє на i-ту точку. Разом з 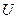вона залежить лише від координат всіх матеріальних точок, а не від їх швидкостей. Рівняння (3) тому показують, що і вектори прискорення матеріальних точок є функціями тільки від координат.

До цього часу мова йшла тільки про замкнуті системи. Розглянемо тепер незамкнуту систему А, що взаємодіє з іншою системою В, яка здійсню заданий рух. В такому випадку говорять, що система А рухається в заданому зовнішньому полі(створюваному системою В). Так як рівняння руху отримуються з принципу найменшої дії шляхом незалежного варіювання кожної з координат(тобто неначе вважаючи інші відомими), ми можемо для знаходження функції Лагранжа 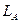системи А, скориставшись лагранжевою функцією 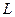всієї системи А+В, замінивши в ній координати заданими функціями часу.

Вважаючи систему А+В замкнутою, будемо мати:

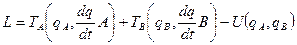, (5)

де перші два члени є кінетичними енергіями систем А і В, а третій член – їх спільну потенціальну енергію.

Підставивши замість задані функції часу і відкинувши члени , що залежить тільки від часу(і тому є повною похідною від деякої іншої функції часу) отримаємо

(6)

Таким чином, рух системи у зовнішньому полі описується функцією Лагранжа звичайного типу з тією відміною, що тепер потенційна енергія може залежати від часу явно.

Так для руху однієї частинки у зовнішньому полі загальний вигляд функції Лагранжа

(7)

і рівняння руху

(8)

Однорідним називають поле, у всіх тачках якого на частинку діє одна і та ж сила 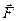. Потенціальна енергія в такому полі дорівнює, очевидно:

(9)

На закінчення зробимо зауваження з приводу застосування рівнянь Лагранжа до різних конкретних задач. Часто доводиться мати справу з такими механічними системами, в яких взаємодія між тілами(матеріальними точками) має, як кажуть, характер зв’язків, тобто обмежень, що накладаються на взаємне розміщення тіл. Фактично такі зв’язки здійснюються шляхом скріплення тіл різними стержнями, нитками, шарнірами і т.п. Ця обставина вносить в рух новий фактор – рух тіл супроводжується тертям в місцях їх дотику, в результаті чого задача виходить за рамки механіки. Але в багатьох випадках тертя в системі виявляється настільки слабким, що його впливом на рух можна повністю знехтувати. Якщо до того ж можна знехтувати масами елементів системи, що скріплюють, то роль останніх зведеться просто до зменшення числа ступенів вільності системи (в порівнянні з числом 3 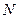). Для визначення її руху можна при цьому знову користуватись функцією Лагранжа виду (1) з числом незалежних узагальнених координат, що відповідають фактичному числу ступенів вільності.