Главная | Обратная связь

Способы получения поляризованного света

Во многих прозрачных кристаллах наблюдается явление двойного лучепреломления – раздваивания падающего на кристалл светового пучка, при котором на выходе из кристалла получается два световых луча (рис. 3.3). Эти лучи являются плоскополяризованными во взаимно перпендикулярных плоскостях.

Один из этих лучей подчиняется обыкновенному закону преломления: показатель преломления этого луча не зависит от направления распространения луча в кристалле, и скорость распространения такого луча одинакова по всем направлениям. Такой луч называют обыкновенным или -лучом.

Показатель преломления второго луча меняется при изменении направления его распространения в кристалле. Скорость распространения данного луча в кристалле зависит от его направления. Такой луч называют необыкновенным или 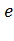-лучом ).

 

Рис. 3.3

В анизотропном кристалле имеется направление, вдоль которого скорости распространения обыкновенного и необыкновенного лучей совпадают. Его называют оптической осью кристалла. Количество оптических осей зависит от типа симметрии кристалла. Кристаллы с одной оптической осью называются одноосными (например, исландский шпат, кварц). Если в кристалле две оптические оси, то он называется двуосным кристаллом (к примеру, слюда).

Устройства, изготавливаемые из анизотропных кристаллов, предназначенные для получения поляризованного света, называют поляризаторами. Если поляризатор применяется для анализа поляризованного света, его называют анализатором. Для изготовления поляризаторов (анализаторов) применяют анизотропные кристаллы с двойным лучепреломлением.

Из исландского шпата изготавливают призмы Николя (или, просто, николи). Николь – это две призмы, склеенные канадским бальзамом.
Падающий на переднюю грань призмы естественный луч раздваивается на обыкновенный и необыкновенный. Обыкновенный луч на границе «шпат – канадский бальзам» претерпевает полное внутреннее отражение, так как канадский бальзам ( ) является для него средой менее плотной, чем исландский шпат ( ), а затем поглощается зачерненной боковой поверхностью призмы. Из николя выходит параллельно падающему один поляризованный необыкновенный луч. Призмы, устроенные подобным образом, называют поляризационными.

В двоякопреломляющих призмах используют различие в показателях преломления обыкновенного и необыкновенного лучей, чтобы развести их возможно дальше друг от друга. Примером таких призм могут служить призмы из исландского шпата и стекла, призмы, составленные из двух призм из исландского шпата со взаимно перпендикулярными оптическими осями.

Для получения поляризованного света также используют двоякопреломляющие кристаллы, обладающие дихроизмом. Дихроизм – это неодинаковая степень поглощения обыкновенного и необыкновенного лучей света. В таких дихроичных кристаллах коэффициент поглощения света
зависит от ориентации вектора . Например, из кристалла турмалина толщиной всего 1 мм выходит только необыкновенный луч. Еще сильнее поглощает один из лучей сернокислый йод-хинин (герапатит). Осаждая на целлулоидную пленку одинаково ориентированные кристаллики герапатита, можно получить поляризатор, поглощающий обыкновенный луч уже при толщине пленки 0,1 мм. Такие поляризационные устройства называются поляроидами.

Лазерное излучение в большинстве случаев линейно поляризовано. Частично поляризованным является свет, излучаемый жидкокристаллическими экранами часов, мониторов и т. д. Кроме этого частично поляризованные лучи получаются при отражении и преломлении света на границе раздела двух диэлектриков, даже тогда, когда обе среды оптически изотропны. В этом случае анизотропией обладают не вещества – имеет место анизотропия условий распространения. Как показывает опыт, в отраженном луче преобладают колебания светового вектора , перпендикулярные плоскости падения, в преломленном луче – колебания, параллельные плоскости падения.

 

Закон Малюса

При пренебрежении ослаблением света за счет потерь на поглощение, отражение и рассеяние, интенсивность света 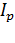, прошедшего поляризатор ,в 2 раза меньше интенсивности естественного света, падающего на него:

 

 

Если разложить каждый из векторов в естественном луче (эти векторы, напомним, имеют всевозможные ориентации) на две компоненты 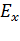и , а затем просуммировать соответствующие векторы (рис. 3.4), то
ввиду равновероятности ориентаций векторов , суммы компонент всех векторов напряженности будут равны. А значит, будут равны и интенсивности соответствующих компонент. Через поляризатор пройдет только та составляющая вектора , которая параллельна его оси. Следовательно, интенсивность луча, прошедшего через поляризатор, будет равна половине интенсивности падающего на него естественного света.

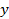
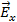
Рис. 3.4

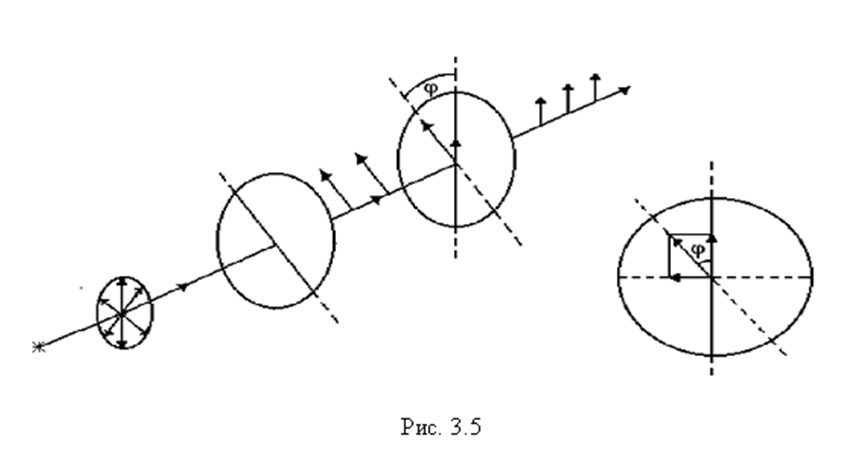
Чтобы убедиться в том, что световой луч при выходе из поляризатора поляризован, и выяснить направление его поляризации, на пути луча ставят анализатор. Если плоскости пропускания анализатора и поляризатора параллельны друг другу, то поляризованный свет пройдет через анализатор без изменения интенсивности (если поглощением света средой можно пренебречь). Если же плоскости поляризатора и анализатора перпендикулярны друг другу, то анализатор полностью погасит падающий на него поляризованный луч. В этом случае говорят, что поляризатор и анализатор скрещены. В промежуточных случаях интенсивность света, прошедшего через анализатор, будет зависеть от взаимной ориентации осей поляризатора. Разберем этот вопрос подробнее.

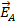
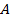
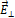
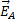
Рис. 3.5

Обозначим амплитуду вектора напряженности электрического поля
в луче, прошедшем через поляризатор, как (рис. 3.5). Пусть ось поляризатора составляет с осью анализатора угол . Разложим вектор на две составляющие: параллельную плоскости анализатора 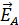и перпендикулярную к ней . Это соответствует разложению волны, в которой совершаются колебания в плоскости , на две волны, поляризованные во взаимно перпендикулярных плоскостях. Одна из них пройдет через анализатор, а волна с колебаниями светового вектора в перпендикулярной плоскости погасится. Из рис. 3.5 следует, что модуль вектора 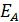при выходе света из анализатора

 

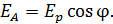
Отношение интенсивностей света пропорционально отношению квадратов амплитуд векторов напряженности электрического поля:

 

 

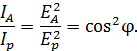
Следовательно,

 

Полученное уравнение выражает закон Малюса: интенсивность света, прошедшего через анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла между осями поляризатора и анализатора.

При скрещенном положении поляризатора и анализатора угол между их осями равен 90^о и свет через анализатор не проходит. Если же оси поляризатора и анализатора параллельны (угол между осями в этом случае равен нулю, а косинус угла – единице), то интенсивность света, прошедшего анализатор, равна интенсивности света, падающего на него.

Если через анализатор пропускать частично поляризованный свет, то интенсивность 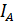прошедшего через него света будет меняться в зависимости от положения оси анализатора, а добиться полного гашения луча никогда не получится. Интенсивность света достигнет максимального значения, если ось анализатора и плоскость преимущественных колебаний частично поляризованного света совпадают. Если же эти плоскости перпендикулярны друг другу, то интенсивность света, прошедшего через анализатор, будет минимальной.

 

Закон Брюстера

 

При падении естественного света на границу раздела двух изотропных диэлектриков отраженный и преломленный лучи света частично поляризуются. Однако при определенном угле падения a_Б, удовлетворяющему условию

 

 

где – относительный показатель преломления среды, равный отношению абсолютных показателей преломления обеих сред ( 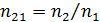), отраженный луч оказывается полностью поляризованным. В отраженном луче содержатся только колебания вектора , перпендикулярные плоскости падения, отмеченные точками на отраженном луче , который приведен на рис. 3.6, а. При этом преломленный луч поляризован частично, и в нем преобладают колебания вектора , параллельные плоскости падения.

Рис. 3.6

а

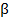
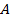
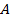
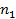
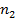
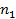
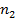
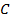
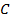
б

Сформулируем закон Брюстера: при падении света на границу
раздела двух диэлектриков под углом, тангенс которого равен относительному показателю преломления этих сред, отраженный луч полностью поляризован, преломленный луч – частично поляризован. Угол между преломленным и отраженным лучами в этом случае равен 90^о.

Такой угол падения света называют углом полной поляризации или углом Брюстера. Этот угол имеет определенное значение для каждого диэлектрика. Для угла Брюстера отраженный и преломленный лучи взаимно перпендикулярны.

Согласно закону преломления света

 

 

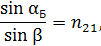
где 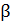– угол преломления. По закону Брюстера

 

 

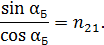
Следовательно, , . Так как угол падения равен углу отражения, то и сумма угла падения и угла отражения также равна 90^о, а значит, угол между отраженным и преломленным лучами составляет 90^о.

Рис. 3.7

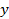
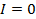
Можно дать следующее объяснение закону Брюстера. Падающий на границу раздела двух диэлектриков естественный свет можно представить в виде двух плоскополяризованных волн, векторы и 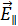которых лежат во взаимно перпендикулярных плоскостях. Одна компонента 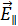лежит в плоскости падения (стрелки на рис. 3.6, а), а другая компонента перпендикулярна плоскости падения (точки на рис. 3.6, а).

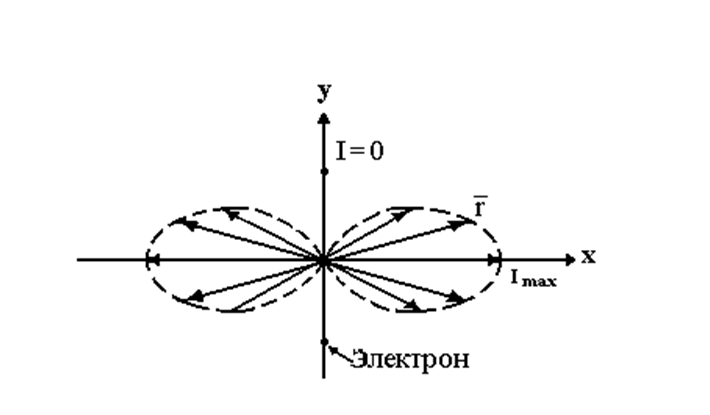
При проникновении световой волны в диэлектрик, ее электрическое поле вызывает вынужденные колебания электронов, принадлежащих атомам (или молекулам) второй среды. Колебания электронов совершаются
в направлениях, совпадающих с направлениями вектора , т. е. происходят в плоскости падения и перпендикулярно ей. Колеблющийся электрон излучает вторичную электромагнитную плоскополяризованную волну, интенсивность которой зависит от направления распространения этой волны, и может быть представлена полярной диаграммой излучения (рис. 3.7).

Здесь радиус-вектор характеризует величину интенсивности излучения в определенном направлении. Как видно из диаграммы, вдоль оси колебания электрона излучение отсутствует, а вдоль направления, перпендикулярного этой оси, оно максимально. При падении поляризованного света на диэлектрик под углом Брюстера (см. рис. 3.6, б) отраженный луч перпендикулярен преломленному , а луч совпадает с направлением колебаний вектoра 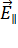и направлением колебаний электронов, колеблющихся в плоскости падения. Следовательно, эти электроны не излучают энергии вдоль . По этой причине отраженный свет на рис. 3.6, б в направлении отсутствует.