 |
|
Анализ поляризованного света
Пусть на кристаллическую пластинку толщиной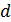 
, вырезанную параллельно оптической оси, нормально падает луч плоскополяризованного монохроматического света длиной волны 
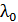в вакууме. Внутри пластинки преломления света не происходит, так как луч падает перпендикулярно пластинке. Обыкновенный и необыкновенный лучи, не разделяясь пространственно внутри пластинки, распространяются с разными скоростями, и на выходе из кристалла происходит сложение колебаний этих двух лучей, поляризованных во взаимно перпендикулярных направлениях. Оптическая разность хода этих лучей, возникающая из-за различия показателей преломления обыкновенного 
и необыкновенного 
лучей, вычисляется по формуле
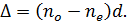
Разность фаз, обусловленная этой разностью хода, будет
Рассмотрим сложение взаимно перпендикулярных колебаний одинаковой частоты. Колебания электрических компонент, поляризованных в перпендикулярных направлениях электромагнитных волн, описываются гармоническими функциями
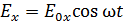
где 
, 
– амплитуды складываемых колебаний.
Для получения уравнения результирующего колебания выразим косинусы из обоих уравнений:
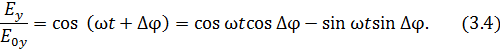
Из основного тригонометрического тождества имеем
Заменим теперь 
и 
в выражении (3.4) полученными выражениями (3.3) и (3.5):
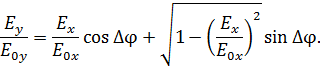
Перенесем второе слагаемое в левую часть уравнения, а выражение, стоящее в левой части уравнения, – в правую. Затем, возводя обе части равенства в квадрат, получим
Из полученного выражения следует уравнение результирующего колебания, возникающего на выходе из кристалла:
Данное уравнение есть уравнение эллипса, оси которого составляют угол 
с декартовыми осями 
и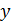 
.
Итак, на выходе из пластинки в результате сложения двух поляризованных во взаимно перпендикулярных направлениях волн возникают световые волны, вектор 
в которых меняется так, что его конец описывает со временем эллипс, уравнение которого было получено. Таким образом, из плоскополяризованного света получается свет поляризованный эллиптически.
Если оптическая разность хода обыкновенного и необыкновенного лучей
то возникающая при этом разность фаз колебаний в обыкновенном и
необыкновенном лучах станет равной 
и уравнение эллипса примет канонический вид
Вырезанная параллельно оптической оси пластинка, для которой оптическая разность хода лучей
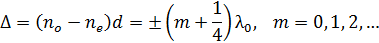
называется пластинкой в четверть длины волны. Плоскополяризованный свет, пройдя пластинку в четверть длины волны, на выходе превращается
в эллиптически поляризованный.
В циркулярно поляризованном свете разность фаз между двумя взаимно перпендикулярными колебаниями равна . Если на пути такого света поставить пластинку в четверть длины волны, то она внесет дополнительную разность фаз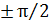 
. Следовательно, циркулярно поляризованный свет, пройдя пластинку в четверть длины волны, станет линейно поляризованным. Если поставить на его пути поляризатор, то при его вращении можно добиться полного гашения светового луча. Если на такую пластинку падает естественный свет, то при прохождении свет останется естественным.