Главная | Обратная связь

Спектральное представление сигналов

 

При анализе процессов прохождения сигналов через тракт радиотехнических устройств используют параметр ширина спектра сигнала – диапазон частот, в пределах которого сосредоточена определенная доля энергии сигнала. Ширину спектра сигнала определяет распределение амплитуд отдельных гармонических составляющих в его спектральной характеристике. Этот параметр сигнала позволяет определить полосу пропускания радиотехнического устройства, обеспечивающую на его выходе минимальные искажения сигнала. На практике полоса пропускания определяется не всем спектром сигнала, а той его частью, в которой сосредоточена наибольшая часть энергии сигнала.

1.3.1. Спектр периодических сигналов. Из математического анализа известно, что периодическую функцию, удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. Поэтому любой сложный, физически реализуемый, периодический сигнал с периодом Т можно представить в виде бесконечного набора гармонических составляющих, частоты которых кратны частоте :

, (1.1)

. (1.2)

Для удобства анализа спектры таких сигналов представляют рядами Фурье, имеющими вид

. (1.3)

 

Здесь амплитуда и начальная фаза n-й гармоники соответственно равны

, . (1.4)

Из (1.3) видно, что спектр периодического сигнала является дискретным. Он содержит постоянную составляющую величиной , основную (первую) гармонику с частотой и высшие гармоники с частотами, кратными частоте .Для наглядности часто зависимость амплитуд и начальных фаз от частоты изображают в виде графиков, которые называются амплитудным и фазовым спектром или амплитудной и фазовой спектральной диаграммами.

В теории радиотехнических сигналов широко используется комплексная форма ряда Фурье, которая получается из (1.1) заменой гармонических функций косинуса и синуса по формулам Эйлера экспоненциальными функциями мнимого аргумента:

. (1.5)

 

Здесь коэффициент – комплексная амплитуда n-й гармоники, которая при положительных и отрицательных значениях индекса n определяется соотношениями

, (1.6)

. (1.7)

 

При отрицательных значениях индекса n комплексная форма ряда Фурье порождает понятие отрицательной частоты.

 

1.3.2. Спектр непериодических сигналов.Спектральное представление непериодического сигнала получим следующим образом: выражение (1.7) для коэффициента подставим в (1.5) и устремим период T в бесконечность. При и суммирование по n заменится интегрированием по . В результате получим:

 

, (1.8)

 

где – спектральная плотность, непрерывная комплексная функция, модуль которой определяет спектральную плотность амплитуд, а аргумент – спектральную плотность начальных фаз. Из (1.8) следует, что спектральная плотность определяется прямым преобразованием Фурье непериодического сигнала

, (1.9)

 

а сам сигнал по его спектральной плотности определяется обратным преобразованием Фурье

. (1.10)

 

Поскольку спектральная плотность – непрерывная функция, то спектр непериодических сигналов называют непрерывным.

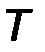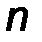Пример 1. Найдем спектр периодической последовательности прямоугольных импульсов с амплитудой А, длительностью импульсов и периодом следования импульсов . Для определения комплексных амплитуд гармоник воспользуемся соотношением (1.7). Выбрав положение импульса, симметричное относительно , и выполнив интегрирование по периоду в пределах , находим амплитуду -той гармоники:

 

,

 

которая в данном случае является вещественной. Спектральное представление периодической последовательности прямоугольных импульсов имеет вид:

 

.

 

На рис. 1.1 показан спектр амплитуд периодической последовательности прямоугольных импульсов для случая А=1 при скважности импульсов .

Рис. 1.1. Спектр амплитуд периодической последовательности прямоугольных импульсов

Пример 2. Найдем спектр одиночного прямоугольного импульса с амплитудой А и длительностью импульса . Для определения спектральной плотности импульса воспользуемся формулой (1.9). Выбираем положение импульса симметричное относительно . Выполнив интегрирование в пределах 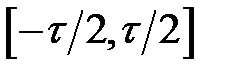, получим:

.

 

График спектральной плотности одиночного импульса при А=1 и =1 приведен на рис. 1.2. Из этого графика видно, что в пределах главного лепестка

 

Рис. 1.2. Спектральная плотность одиночного импульса при А=1 и =1

 

сосредоточена значительная доля энергии сигнала (более 90%). Граничная частота главного лепестка ω₀₁ определяется формулой

 

ω₀₁ =2π/ τ.

Из неё следует, что чем короче импульс, тем шире его спектр. На практике ширину полосы пропускания Δω выбирают приближенным соотношением

Δω= (2÷3) ω₀₁.

 

2. ОСНОВНЫЕ ПОЛОЖЕНИЯ

ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ