 |
|
Гармонические сигналы и их представление
Сигналы, которые описываются тригонометрическими функциями 
или 
называются гармоническими. Гармонический сигнал можно представить в виде
,
где 
– амплитуда; 
– круговая частота; 
– начальная фаза; 
– полная фаза (фазовый угол). Круговая частота связана с циклической частотой 
и периодом колебания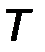 
соотношением 
.
Гармонические сигналы обладают замечательным свойством: результирующее колебание при линейных операциях – алгебраическом сложении любого числа гармонических колебаний одинаковой частоты, дифференцировании, интегрировании – есть гармоническое колебание той же частоты. Это свойство объясняет широкое применение гармонических сигналов в измерительной аппаратуре в качестве тестовых.
Техника определения параметров результирующего колебания значительно упрощается, если при описании гармонического сигнала вещественную тригонометрическую функцию заменить комплекснозначной экспоненциальной функцией. Вещественному сигналу ставится в соответствие комплексный сигнал:
,
где 
– мнимая единица; 
– комплексная амплитуда колебания. Она содержит информацию об амплитуде колебания и о его начальной фазе. Множитель 
описывает временную зависимость колебания.
Поскольку при всех линейных операциях частота гармонического сигнала сохраняется и всегда известна, то остается анализировать только изменения, которые претерпевают амплитуда и фаза сигнала.
Для наглядности часто мгновенные значения комплексных амплитуд сигналов и результат их линейного преобразования изображают векторами на комплексной плоскости. Такое представление называется векторной диаграммой.
Представление гармонического сигнала в комплексной форме составляет основу метода комплексных амплитуд, который широко используется в радиотехнике и электротехнике при анализе линейных цепей.