Главная | Обратная связь

Математические методы решения задачи ЛП

Симплекс метод

Оптимальное решение ЗЛП связано с угловыми точками на границах многогранника решений. Конечная граница многогранника решений или количество опорных планов определяется числом сочетаний

С_n^m = п!/m!(n-m)!.

Если п=50, m=25 то число базисных планов 10¹⁴. При больших m и nнайти оптимальный план, перебирая все опорные планы задачи очень трудно и трудоемко. Поэтому необходимо иметь схему позволяющую переходить от одного опорного плана к другому. Такой схемой называется симплексный метод, который позволяет за конечное число шагов получить ее оптимальный план. Каждый из шагов состоит в нахождении нового плана, которому соответствует меньшее или большее значение целевой функции, чем значение этой же функции в предыдущем плане. Процесс продолжают до получения оптимального плана. Если задача не имеет оптимального решения, то симплексный метод позволяет установить это в процессе решения.

Построение опорных планов. Пусть поставлена ЗЛП.

Найти минимальное значение функции

F = C₁X₁ + C₂X₂ + ... + C_nX_n (5.1)

при ограничениях

 

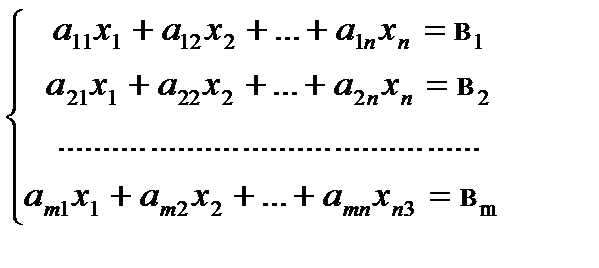(5.2)

где

х_j >=0, (i=1,2,...,m). (5.3)

 

Предположим, что система ограничений задачи m единичных векторов, причем ими являются первые m векторов. Тогда

F = C₁X₁ + C₂X₂ + ... + C_nX_n (5.4)

при ограничениях

 

(5.5)

x_j >=0, j = 1,2, ..., n. (5.6)

 

Запишем систему (2.35) в векторной форме:

х₁А₁+х₂А₂+... + х_mA_m + x_m+1A_m+1+ ... x_nA_n= В (5.7)

, , …, , ,….,

,

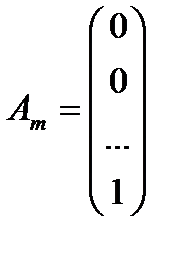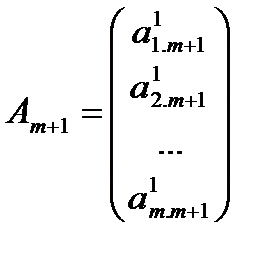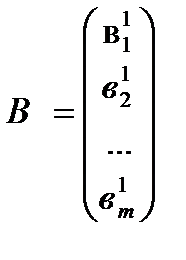
Векторы А_1, А_2, ... А_m- линейно независимые единичные векторы m мерного пространства. Они образуют базис этого пространства. Поэтому в разложении (7) за базисные переменные выбираем х₁,х₂, ... х_m,свободные неизвестные х_m+1,х_m+2, ... х_nприравниваем нулю и, учитывая, что в_i>=0 (i=1,2,...m), а векторы А_1, А_2, ... А_m -единичные,получаем первоначальный план:

х₀ = (х₁=в₁; х₂=в₂; ... х_m=в_m; х_m+1=0; ... x_n=0) (5.8)

Плану (2.38) соответствует разложение

 

х₁А₁+х₂А₂+... + х_mA_m = В (5.9)

где векторы А_1, А_2, ... А_m линейно независимы, следовательно, построенный план является и опорным.

Определение 1.Решение системы ограничений (5.2), соответствующее нулевым значениям свободных неизвестных, называются базисным.

Рассмотрим, как, исходя из первоначального опорного плана (5.8), можно построить второй опорный план. Предположим, что для некоторого вектора, не входящего в базис, например А_m+1,является положительным хотя бы один из коэффициентов х_i,m+1 в разложении

 

х_1,m+1А₁+х_2,m+1А₂+... + х_m,m+1A_m = A_m+1

 

Правую часть В разделим на положительные коэффициенты этой переменной, т.е. в_i/a_im+1.Таким образом, вектор х_m+1является планом или новым базисом. Задача может иметь не более m базисов, поэтому один из существующих базисов исключаем. Для этого выбираемQ= min (в_i/a_i,m+1). Пусть эта компонента стоит на первом месте, т.е. Q₁=min (в₁/a_1,m+1).Тогда получим новое базисное решение Х=( х₂, х₃,...х_m,x_m+1).Это означает, что х₁нужно исключить из базиса, а включить в базисх_m+1 . Таким образом, процесс получения новых опорных планов заключается в выборе вектора, который подлежит включению в базис, и определении вектора, подлежащего исключению из базиса.

Условия оптимальности.Предположим, что ЗЛП имеет базисное решение. В этом случае имеем

 

х₁А₁+х₂А₂+... + х_mA_m = В (5.10)

х₁С₁+х₂С₂+... + х_mС_m = F (5.11)

где все х_i>0,aF - значение функции, соответствующее этому плану. Если коэффициент С_j в линейной функции соответствует векторуA_j, то F_j -C_jназывается критерием оптимальности или оценкой линейной функции. Критерий оптимальности равен сумме стоимостей деятельности, которые исключают из программы, минус доход от единицы продукта, вводимого в план. F_j -сумма произведений коэффициентов при переменных уравнения целевой функции на коэффициенты при переменных в ограничениях, т.е.

F_j= е c_j a_ij

^{iÎ I}

c _j - коэффициенты при переменных уравнения целевой функции.

Справедливы следующие теоремы.

Теорема 1.Если для некоторого вектора А_j выполняется условие

F_j -C_j>=0,

то план Х₀ является оптимальным для максимального значение функции.

Теорема 2.Если для некоторого вектора А_j выполняется условие

F_j -C_j>=0,

то план Х₀ является оптимальным для минимального значения функции.

Таким образом, для того чтобы план задачи на отыскание максимального значения линейной функции был оптимальным, необходимо и достаточно, чтобы его оценки были положительными. А для отыскания минимального значения функции, необходимо и достаточно, чтобы его оценки были отрицательными.

Таким образом, решение задачи симплексным методом проводится по следующей схеме:

1) строится базисное решение;

2) с помощью признака оптимальности проверяется, не является ли это решение оптимальным;

3) если нет, то строится другое базисное решение, более близкое к оптимальному;

4) повторяется второй пункт до тех пор пока не выполняется условие оптимальности.

Доказано, что в результате конечного числа перебора вариантов можно получить наилучшее; т.е. оптимальное решение.