Главная | Обратная связь

Бисериальный коэффициент корреляции.

Данный КК вычисляется, когда одна переменная измерена в номинальной дихотомической шкале (0 или 1), а вторая переменная в количественной шкале. Одним из способов описания связи между такими переменными является просто вычисление КК Пирсона по исходным данным. Однако можно воспользоваться более простой формулой для вычисления. В этом случае КК называется точечный бисериальный КК и обозначается prb. Он вычисляется по следующей формуле:

rpb = (x 1 – x 0) : Sx (n1 n0 : n (n – 1)) , где x 1 – среднее значение для тех лиц, у которых номинальная переменная у = 1; x 0 – среднее значение для тех лиц, у который номинальная переменная у = 0; Sx – стандартное отклонение для значений по переменной х; n1 – количество лиц, для которых переменная у = 1; n0 – количество лиц, для которых переменная у = 0; n – общее количество лиц, т.е. n = n1 + n0.

Этот КК называется бисериальным, т.к. фактически имеется две серии лиц. Одна серия лиц, для которых номинальная переменная у = 1,а вторая серия лиц, для которых номинальная переменная у = 0.

Пример вычисления бисериального КК.

Пусть переменная х – это рост в см, а переменная у – это пол (1 – мальчики, 0 – девочки). В эксперименте участвовали 15 подростков. Были получены следующие результаты:

х	у
150 170 160 165 140 183 157 152 163 168 180 155 157 160 152	1 0 1 1 0 1 0 0 1 1 1 0 1 0 0

n = 15 n1 = 8 n0 = 7

x 1 = (150+160+…+157) : 8 = 163,25

x 0 = (170+140+…+152) : 7 = 156,57

x = 8,94

rpb = (163,25 – 156,57) : 8,94 8 7; (15 (15 – 1)) = 0,41

n = 15 = 0,05

t набл = n – 2 rpb : 1 – rpb = 15 – 2 0,41 : 1 – (0,41) = 1,62

/2 = 0,05/2 = 0,025 = n – 2 = 15 – 2 = 13 tкр = 2,16

12.1. Нормальное распределение и его свойства.

Теория вероятностей и математическая статистика исследуют законы, описывающие поведение случайных величин, как дискретных, так и непрерывных. Такие законы отражают оценку вероятности того или иного значения случайной величины, что обычно обозначают как распределение случайной величины.

Нормальное распределение имеет место тогда, когда интересующее нас явление подвержено влиянию бесконечного числа случайных факторов, уравновешивающих друг друга.

 

 

При обработке данных измерений в науке и технике обычно предполагают нормальный закон распределения случайных погрешностей измерений. Оно всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия множества причин, каждая из которых дает малыйвклад в погрешность. Причем совершенно неважно, по какому закону распределен каждый из вкладов в отдельности.

Свойства нормально распределенной случайной величины x:

 

1. ;

2. ρ(x) является непрерывной функцией;

3. Центр распределения случайной величины одновременно является центром симметрии;

4. Малые отклонения встречаются чаще больших, другими словами, реализуются с большей вероятностью.

Вероятность того, что результат измерения попадет в интервал [x₁,x₂], равна:

В скобках после P указано событие, для которого вычислена вероятность. При увеличении границ промежутка в обе стороны до бесконечности интеграл от функции распределения

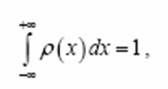
т.е. попадание результата измерения в диапазон является достоверным событием.

12.2.Единичным (стандартным) нормальным распределением (z-распределением) называется такое нормальное распределение, математическое ожидание для которого равно 0, а дисперсия 1.

 

 

 

Случайные величины связаны со случайными событиями.

О случайных событиях говорят тогда, когда оказывается невозможным однозначно предсказать результат, который может быть получен в тех или иных условиях.

Дискретная:

Может принимать конкретные значения из ограниченного множества. Набор значений ограничен, фиксирован.

Непрерывная:

Может принимать неопределенный набор значений из фиксированного множества. Набор значений неограничен, случаен.

Единичное нормальное распределение устанавливает четкую взаимосвязь стандартного отклонения и относительного количества случаев в генеральной совокупности для любого нормального распределения. Например, зная свойства единичного нормального распределения, мы можем ответить на следующие вопросы. Какая доля генеральной совокупности имеет выраженность свойства от о до +1? Какова вероятность того, что случайно выбранный представитель генеральной совокупности будет иметь выраженность свойства, превышающую среднее значение?