Главная | Обратная связь

Метод Бубнова-Гальоркіна

Метод Бубнова—Гальоркіна заснований на властивості ортогональності функцій. У курсі математичного аналізу дається наступне визначення ортогональних функцій: якщо є сімейство безперервних функцій

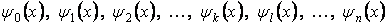(а)

і інтеграл добутку будь-яких двох різних функцій цього сімейства в проміжку дорівнює нулю:

(6.6)

ці функції (а) утворять у цьому проміжку ортогональну систему. Наприклад, сімейство тригонометричних функцій

(б)

є ортогональною системою в проміжку

Дійсно,

(в)

причому, ці інтеграли вичерпують усілякі варіанти комбінування двох різних функцій сімейства (б).

На підставі леми з курсу математичного аналізу слідує: якщо одна з функцій тотожно дорівнює нулю, наприклад , то вона ортогональна до всіх без винятку функцій, тому що в цьому випадку виконується умова (6.6). Як приклад можна привести функцію

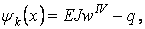
(г)

яка представляє собою ліву частину диференціального рівняння вигнутої осі балки. Ця функція тотожно рівна нулю при будь-яких значеннях x, і, відповідно,

Тут інтеграл береться по всій довжині балки L, і тому функція (г) ортогональна в проміжку до будь-якої функції.

Якщо функцію прогинів замінити її наближеним виразом у формі ряду

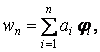
(д)

то функція (г) уже не буде тотожно дорівнює нулю, а виходить, і не буде ортогональна в зазначеному проміжку до будь-якої функції. Можна, однак, зажадати, щоб вона була ортогональна хоча б до обмеженого класу функцій, наприклад функцій , що становлять ряд (д), тобто щоб

(е)

У результаті одержимо n лінійних рівнянь для визначення n постійних коефіцієнтів , що входять у ряд (д).

На використанні системи рівнянь (е) для визначення значень параметрів і заснований метод Бубнова-Гальоркіна. Всі міркування, наведені для функції одного аргументу, можна застосувати й до функцій двох аргументів і більше. Для розв’язання задач про вигин пластинок рівняння Бубнова-Гальоркіна (е) можна представити у вигляді

(6.7)

де замість лінійного проміжку розглядається плоска область s, обмежена контуром пластинки, а функція 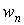виражається наступним подвійним рядом по області s:

(ж)

Таким чином, наближена функція в рівняннях (6.7), що представляє собою ліву частину диференціального рівняння вигнутої серединної поверхні пластинки (5.16), ортогональна в області s до всіх функцій 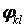ряду (ж), що входить у цю наближену функцію.

Методу Бубнова-Гальоркіна можна дати й інше, тлумачення. Функція являє собою проекцію на вісь z всіх зовнішніх і внутрішніх сил, що діють на нескінченно малий елемент пластинки. Функція прогинів 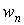є переміщення в напрямку тої ж осі. Виходить, функції 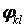теж є переміщеннями в напрямку осі z і їх можна вважати можливими переміщеннями. Отже, рівняння Бубнова-Гальоркіна (6.7) приблизно виражають рівність нулю роботи всіх зовнішніх і внутрішніх сил у пластинці на можливих переміщеннях .

Таким чином, метод Бубнова-Гальоркіна, як і метод Рітца-Тимошенко, виходить із принципу можливих переміщень, обидва методи рівноправні. В обох випадках апроксимуючу функцію необхідно вибирати так, щоб вона задовольняла геометричним граничним умовам. Виконання статичних умов не обов'язково.

Метод Власова

З варіаційних методів приведення диференціальних рівнянь у частинних похідних до звичайних диференціальних рівнянь зупинимося ще на методі В. 3. Власова.

У досліджуваній пластинці будемо розрізняти два напрямки: поперечний, співпадаючий з напрямком осі , і поздовжній, співпадаючий з напрямком осі . На поздовжніх краях можуть бути дані граничні умови, як геометричні, так і статичні, всього по дві умови на кожному краї. При кожному функція прогинів пластинки 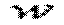описує безперервну вигнуту лінію , що задовольняє на кінцях (на поздовжніх краях пластинки) заданим геометричним граничним умовам. Нехай ця лінія представлена за допомогою n лінійно незалежних функцій 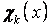, що задовольняють тим же геометричним граничним умовам, що й , тобто

(а)

Функції 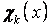є безрозмірними, а коефіцієнти мають розмірність прогину .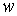

Переходячи від лінії до іншої, суміжної з нею, зауважуємо, що внаслідок безперервності функції 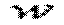значення числових коефіцієнтів будуть мінятися як безперервні функції y. Отже, функція прогинів може бути представлена у вигляді розкладання

(б)

Одну із двох систем функцій — або 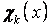— можна вибрати заздалегідь і надалі вважати заданою. Будемо вважати таку систему безрозмірних функцій 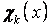. Тоді функції , що мають розмірність прогину, будуть шуканими коефіцієнтами розкладання. Відповідно до розмірностей й фізичного змісту формули (б) функції 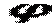називаються узагальненими прогинами, а 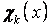— функціями поперечного розподілу прогинів.

Подання вигнутої серединної поверхні пластинки у вигляді розкладання (б) при кінцевому числі n означає, що пластинка замінена системою з кінцевим числом ступенів свободи в поперечному напрямку при збереженні нескінченного числа ступенів свободи в поздовжньому напрямку. Це означає також приведення двовимірної задачі вигину пластинки до одномірної, тому що після того, як знайдені всі n функцій , значення прогинів будуть визначені з відомим ступенем точності.

Вибір функції прогинів у вигляді кінцевого ряду (б) припускає наближений розв’язок задачі. У загальному випадку функція (б) не буде задовольняти рівнянню (5.15). Тому для визначення функцій скористаємося варіаційним методом Бубнова-Гальоркіна. Варіаційне рівняння (6.7) для розв'язуваної задачі можна записати в такій формі:

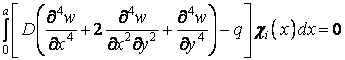
(в)

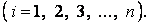
Застосовуючи інтегрування вроздріб, вираз (в) представимо у вигляді

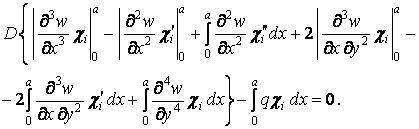
(г)

Відповідно до формул (5.8) і (5.19), різниця значень згинальних моментів і наведених поперечних сил , обчислених для крайових перетинів пластинки , складе:

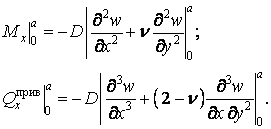
З огляду на ці залежності, рівняння (г) можна трохи спростити:

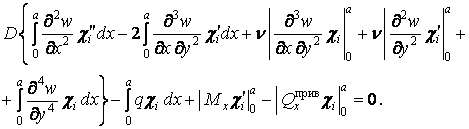
(д)

Вхідні в це рівняння члени 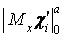і являють собою віднесену до одиниці довжини роботу крайових згинальних моментів і наведених поперечних сил, прикладених у перетинах і . Зараховуючи цю роботу до сумарної роботи зовнішнього навантаження й підставляючи функцію (б), одержимо варіаційне рівняння рівноваги (д) в остаточному вигляді:

(6.8)

Вхідні сюди коефіцієнти обчислюються по формулах

(е)

a вільні члени - по формулі

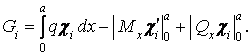
(ж)

Коефіцієнти , , 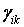визначаються тільки обраною системою функцій поперечного розподілу прогинів . Вони мають властивість взаємності:

(з)

Якщо поздовжні краї пластинки закріплені від прогинів, то формули (е) приймають вигляд

Даючи індексу i у рівнянні (6.8) різні значення від 1 до n, одержимо для визначення невідомих функцій повну систему n звичайних лінійних диференціальних рівнянь із постійними коефіцієнтами. Всі рівняння будуть четвертого порядку щодо кожної шуканої функції . Завдяки властивості взаємності коефіцієнтів (з) система рівнянь буде мати симетричну структуру.

Найбільш ефективним методом інтегрування таких систем є метод, що дозволяє привести систему рівнянь до одному еквівалентного їй диференціального рівняння. У цьому випадку ним буде рівняння порядку 4n. Звідси випливає, що до рівнянь (6.8) повинні бути приєднані 4n граничних умов на поперечних краях.

Розв’язуючи систему рівнянь (6.8) при заданих граничних умовах на поперечних краях, одержимо вирази для всіх функцій і тим самим відповідно до розкладання (б) визначимо функцію прогинів .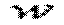

Для визначення зусиль у пластинці перетворимо формули (8.8), (8.9), (8.10) і (8.19), підставивши в них функцію (б):

(6.9)

На закінчення зупинимося на виборі функцій поперечного розподілу прогинів. Вони апроксимують деформації довільної поперечної смужки, вирізаної із пластинки, і можуть бути обрані різними способами, але повинні задовольняти геометричним граничним умовам на поздовжніх краях пластинки й бути лінійно незалежними.

За функції 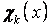можна приймати фундаментальні функції поперечних коливань балки постійного перерізу. Наприклад, при шарнірному обпиранні обох поздовжніх країв і навантаженню, симетричному щодо площини

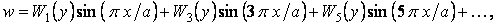
а при кососиметричному навантаженні

Якщо поздовжні краї пластинки вільні від обпирання, то при симетричному навантаженні

а при кососиметричному

Якщо край , шарнірно обпертий, а край вільний від обпирання, то

Можна побудувати функції статичним шляхом. Для цього варто розглянути елементарну смугу пластинки як звичайну балку й для цієї балки відповідно до заданих граничних умов визначити вигнуту вісь від того або іншого поперечного навантаження. Видозмінюючи навантаження, одержимо різні форми вигину балки, тобто різні функції .