 |
|
Вопрос_13 Оптимальный фильтр, обоснование требования к выбору его частотной и фазовой характеристик
Требуется найти такую импульсную переходную функцию h(t) фильтра, которая минимизирует среднюю квадратическую ошибку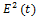 
. Время запаздывания сигнала в фильтре t0=0, x(t) и n(t) – стационарные взаимно некоррелированные процессы с известными спектрами плотности мощности Gx(t) и Gn(t)
Будем искать передаточную функцию этого фильтра в виде
K(f) =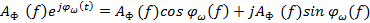 
, где 
– амплитудно и фазо - частотная характеристики фильтра
Искажение сигнала на выходе фильтра при наличии шума состоит из 2 составляющих.
1) – зависит от шума, прошедшего через фильтр. ЕЕ дисперсия
= 
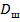2) Вызвана искажениями полезного сигнала фильтром из-за отличия 
от 1
= 
В силу независимости этих искажений, суммарная дисперсная ошибка сигнала равна
= 2 
+2 
=2 
= 
+ 
Значение минимально, когда cos=1
Величина D зависит от 
и будет минимальной при мин значении подынтегрального выражения. Для нахождения минимума найдем производную подынтегрального выражения по и приравняем ее к 0.
Получим 
Отсюда
Это частотная характеристика минимального фильтра, а фазовая 0. Если частотную хар-ку подставить в 
,что получим 
,
<1, 
При использовании оптимальных фильтров вых сигнал будет меньше зашумлен,чем аходной
Если частотная хар-ка шума и сигнала не перекрываются, то шум не влияет на сигнал
Вопрос_14 Импульсная характеристика согласованного фильтра. Определение вых сигнала.
) 
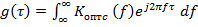Сигнал будет представлять собой зеркальное отображение исходного сигнала
Выходной сигнал согласованного фильтра
Введем новые переменные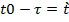 
, то 
Полученный интеграл представляет собой корреляционную функцию. Максимум полезного сингала на выходе согласованного фильтра, достигаемый в момент t=to совпадает с максимумом сигнальной составляющей корреляционного интеграла, достигаемый при 